| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Solved Examples (Examples 1 to 11) | Question 1 to 23 (Multiple Choice Questions) | Question 24 to 59 (Fill in the Blanks) |
| Question 60 to 79 (True or False) | Question 80 to 140 | |
Chapter 7 Comparing Quantities
Welcome to this dedicated resource featuring comprehensive, step-by-step solutions for the NCERT Exemplar problems specifically designed for Class 7 Mathematics, focusing on the vital chapter: Comparing Quantities. It's important to recognize that these Exemplar questions are crafted to move significantly beyond the routine exercises found in the standard textbook. Their primary objective is to enhance students' abilities to apply core concepts such as ratio, proportion, percentage, profit and loss, and simple interest within more challenging, realistic, and multi-faceted scenarios, thereby fostering deeper quantitative reasoning.
The solutions provided here thoroughly cover the diverse methods used for comparing quantities. This includes:
- Utilizing ratios for fundamental comparison and mastering the conversion of ratios into percentages (and vice versa) for standardized comparison.
- Understanding and accurately calculating percentage increase or decrease, a skill essential in analyzing changes in values like prices or populations.
- Tackling complex percentage problems, such as finding the original quantity when only the final value after a percentage increase or decrease is known.
A significant portion of this chapter deals with practical applications in commerce, particularly Profit and Loss. The solutions provide detailed guidance on:
- Calculating Profit (if Selling Price $>$ Cost Price) and Loss (if Cost Price $>$ Selling Price).
- Determining Profit Percentage ($\text{Profit}\% = \frac{\text{Profit}}{\text{Cost Price}} \times 100$) and Loss Percentage ($\text{Loss}\% = \frac{\text{Loss}}{\text{Cost Price}} \times 100$). Remember, profit and loss percentages are always calculated on the Cost Price (CP) unless stated otherwise.
- Solving intricate problems like finding the CP when the Selling Price (SP) and profit/loss percentage are given, or determining the SP required to achieve a certain profit/loss percentage based on a known CP. These solutions also address scenarios involving overhead expenses (which are added to the initial CP) and calculating the overall gain or loss percentage from multiple transactions, potentially involving monetary values in $\textsf{₹}$.
Furthermore, the fundamental concepts of Simple Interest (SI) are thoroughly addressed. The solutions demonstrate:
- Calculating the Simple Interest (SI), the Principal amount (P), the Rate of interest per annum (R), or the Time period (T) using the core formula: $SI = \frac{P \times R \times T}{100}$.
- Calculating the total Amount (A) payable at the end of the time period using the relationship $A = P + SI$.
- Solving Exemplar problems that might require rearranging the SI formula to find an unknown P, R, or T when the other variables are provided, or comparing the simple interest earned under different investment conditions (e.g., different rates or time periods). Calculations often involve sums represented in $\textsf{₹}$.
The Exemplar questions test these concepts through diverse formats including MCQs, Fill-in-the-Blanks, True/False statements, and challenging Short/Long Answer problems demanding multi-step calculations. The provided solutions offer clear, step-by-step workings, explicitly showing the application of formulas, presenting a logical structure for tackling word problems, and emphasizing accuracy (like using the correct base value for percentage calculations). Engaging with this resource will enable students to achieve mastery in applying these crucial quantitative comparison techniques to complex practical problems, thereby enhancing their financial literacy and overall numerical reasoning skills significantly.
Solved Examples (Examples 1 to 11)
In Examples 1 to 3, there are four options, out of which one is correct. Choose the correct one.
Example 1: The ratio of the heights 1.50 m and 75 cm of two persons can be written as
(a) 1 : 50
(b) 1 : 5
(c) 2 : 1
(d) 1 : 2
Answer:
The heights of the two persons are given as 1.50 m and 75 cm.
To find the ratio, we need to express both heights in the same unit.
Let's convert meters to centimeters.
We know that 1 m = 100 cm.
So, 1.50 m = $1.50 \times 100$ cm = 150 cm.
Now, we find the ratio of the two heights:
Ratio = $\frac{\text{Height of first person}}{\text{Height of second person}}$
Ratio = $\frac{150 \text{ cm}}{75 \text{ cm}}$
We can simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 75.
$\frac{150 \div 75}{75 \div 75} = \frac{2}{1}$
The ratio of the heights is 2 : 1.
Comparing this ratio with the given options:
(a) 1 : 50
(b) 1 : 5
(c) 2 : 1
(d) 1 : 2
The correct option is (c) 2 : 1.
Example 2: Out of 50 children in a class, 20 are boys. Then the percentage of girls is
(a) 60
(b) 30
(c) 50
(d) $66\frac{2}{3}$
Answer:
Given:
Total number of children in the class = $50$.
Number of boys = $20$.
To Find:
The percentage of girls in the class.
Solution:
First, we find the number of girls in the class.
Number of girls = Total number of children - Number of boys
Number of girls = $50 - 20 = 30$
Now, we calculate the percentage of girls.
Percentage of girls $= \frac{\text{Number of girls}}{\text{Total number of children}} \times 100\%$
Percentage of girls $= \frac{30}{50} \times 100\%$
Percentage of girls $= \frac{3}{5} \times 100\%$
Percentage of girls $= 0.6 \times 100\%$
Percentage of girls $= 60\%$
The percentage of girls is 60%.
Comparing with the given options, the correct option is (a) 60.
Example 3: The interest on ₹ 5000 at the rate of 15% per annum for one month is
(a) ₹ 750
(b) ₹ 75
(c) ₹ 625
(d) ₹ 62.50
Answer:
Given:
Principal (P) = $\textsf{₹}\ 5000$
Rate of Interest (R) = $15\%$ per annum
Time (T) = 1 month
To Find:
The simple interest for one month.
Solution:
The formula for simple interest is:
$SI = \frac{P \times R \times T}{100}$
where P is the principal amount, R is the annual rate of interest, and T is the time in years.
The given time is 1 month. We need to convert this to years.
$1 \text{ month} = \frac{1}{12} \text{ years}$
Now, substitute the given values into the formula:
$P = 5000$
$R = 15$
$T = \frac{1}{12}$
$SI = \frac{5000 \times 15 \times \frac{1}{12}}{100}$
$SI = \frac{5000 \times 15}{100 \times 12}$
Simplify the expression:
$SI = \frac{\cancel{5000}^{50} \times 15}{\cancel{100}_{1} \times 12}$
$SI = \frac{50 \times 15}{12}$
Simplify further by dividing 15 and 12 by 3:
$SI = \frac{50 \times \cancel{15}^5}{\cancel{12}_4}$
$SI = \frac{50 \times 5}{4}$
$SI = \frac{250}{4}$
Now, perform the division:
$SI = 62.5$
The interest for one month is $\textsf{₹}\ 62.50$.
Comparing with the given options:
(a) $\textsf{₹}\ 750$
(b) $\textsf{₹}\ 75$
(c) $\textsf{₹}\ 625$
(d) $\textsf{₹}\ 62.50$
The correct option is (d) $\textsf{₹}\ 62.50$.
In Examples 4 and 5, fill in the blanks to make the statements true.
Example 4: If two ratios are equivalent, then the four quantities are said to be in ______.
Answer:
If two ratios are equivalent, then the four quantities are said to be in proportion.
Explanation:
A ratio is a comparison between two quantities of the same unit. For example, the ratio of 1 meter to 2 meters is $1:2$ or $\frac{1}{2}$.
Equivalent ratios are ratios that express the same relationship. For instance, the ratio $1:2$ is equivalent to $2:4$, $3:6$, etc., because $\frac{1}{2} = \frac{2}{4} = \frac{3}{6}$.
A proportion is an equation stating that two ratios are equivalent. It is a statement of equality between two ratios.
If we have two ratios, say $a:b$ and $c:d$, and these two ratios are equivalent, we can write this as:
$\frac{a}{b} = \frac{c}{d}$
This statement means that the quantities $a, b, c,$ and $d$ are in proportion.
The four quantities $a, b, c, d$ are called the terms of the proportion. $a$ and $d$ are called the extreme terms (or extremes), and $b$ and $c$ are called the middle terms (or means).
So, when the ratio $a:b$ is equivalent to the ratio $c:d$, the four quantities $a, b, c,$ and $d$ are said to be in proportion.
Therefore, the word that fills the blank is proportion.
Example 5: 40% of 250 km is __________.
Answer:
To find 40% of 250 km, we can express the percentage as a fraction or a decimal and multiply it by the quantity.
Method 1: Using fractions
40% can be written as $\frac{40}{100}$.
So, 40% of 250 km $= \frac{40}{100} \times 250$ km
$= \frac{40 \times 250}{100}$ km
$= \frac{10000}{100}$ km
$= 100$ km
Method 2: Using decimals
40% can be written as $0.40$ or $0.4$.
So, 40% of 250 km $= 0.4 \times 250$ km
$= 100$ km
Alternatively, we can simplify the fraction first:
$\frac{40}{100} = \frac{4}{10} = \frac{2}{5}$
So, 40% of 250 km $= \frac{2}{5} \times 250$ km
$= 2 \times \frac{\cancel{250}^{50}}{\cancel{5}_1}$ km
$= 2 \times 50$ km
$= 100$ km
Therefore, 40% of 250 km is 100 km.
The statement becomes: 40% of 250 km is 100 km.
In Examples 6 and 7, state whether the statements are True or False.
Example 6: If 25% of a journey is 800 km, the total distance of the journey is 3000 km.
Answer:
The statement is False.
Explanation:
Let the total distance of the journey be $D$ km.
According to the given information, 25% of the journey is 800 km.
We can write this as an equation:
$25\%$ of $D = 800$ km
To convert the percentage to a decimal or fraction, we divide by 100:
$\frac{25}{100} \times D = 800$
Simplify the fraction $\frac{25}{100}$ to $\frac{1}{4}$:
$\frac{1}{4} \times D = 800$
To find the total distance $D$, multiply both sides of the equation by 4:
$D = 800 \times 4$
$D = 3200$
The total distance of the journey is 3200 km.
The statement claims that the total distance is 3000 km, which is incorrect.
Since the calculated total distance (3200 km) is not equal to the claimed distance (3000 km), the statement is false.
Example 7: 0.05 is equivalent to 5%.
Answer:
The statement is True.
Explanation:
To convert a decimal to a percentage, we multiply the decimal by 100.
$0.05 \times 100 = 5$
So, 0.05 is equivalent to 5%.
Alternatively, to convert a percentage to a decimal, we divide the percentage by 100.
$5\% = \frac{5}{100} = 0.05$
Since both conversions result in the equality $0.05 = 5\%$, the statement is true.
Example 8: Suhana sells a sofa set for ₹ 9600 making a profit of 20%. What is the C.P. of the sofa set?
Answer:
Given:
Selling Price (SP) of the sofa set = $\textsf{₹}\ 9600$
Profit Percentage = $20\%$
To Find:
The Cost Price (CP) of the sofa set.
Solution:
When there is a profit, the Selling Price (SP) is the Cost Price (CP) plus the profit.
Profit is calculated as a percentage of the Cost Price.
Let the Cost Price (CP) be $\textsf{₹}\ x$.
Profit amount = $20\%$ of CP
Profit amount = $20\%$ of $x$
Profit amount = $\frac{20}{100} \times x = \frac{1}{5} x$
The relationship between SP, CP, and Profit is:
$SP = CP + \text{Profit}$
Substitute the given values and the expression for profit:
$9600 = x + \frac{1}{5} x$
Combine the terms involving $x$:
$9600 = \frac{5x}{5} + \frac{1x}{5}$
$9600 = \frac{5x + 1x}{5}$
$9600 = \frac{6x}{5}$
To solve for $x$, multiply both sides by 5 and divide by 6:
$6x = 9600 \times 5$
$x = \frac{9600 \times 5}{6}$
Simplify the expression. We can divide 9600 by 6:
$\frac{\cancel{9600}^{1600}}{\cancel{6}_1} = 1600$
So,
$x = 1600 \times 5$
$x = 8000$
The Cost Price of the sofa set is $\textsf{₹}\ 8000$.
Alternate Solution (Using Formula):
The formula relating SP, CP, and Profit% is:
$SP = CP \times \left(1 + \frac{\text{Profit}\%}{100}\right)$
Substitute the given values:
$9600 = CP \times \left(1 + \frac{20}{100}\right)$
$9600 = CP \times \left(1 + \frac{1}{5}\right)$
$9600 = CP \times \left(\frac{5}{5} + \frac{1}{5}\right)$
$9600 = CP \times \left(\frac{6}{5}\right)$
To find CP, rearrange the equation:
$CP = 9600 \times \frac{5}{6}$
Simplify the expression:
$CP = \frac{\cancel{9600}^{1600} \times 5}{\cancel{6}_1}$
$CP = 1600 \times 5$
$CP = 8000$
The Cost Price of the sofa set is $\textsf{₹}\ 8000$.
Example 9: John borrowed ₹ 75000 from his friend and after one year returned ₹ 80000 to his friend. Find the interest.
Answer:
Given:
Principal amount borrowed (P) = $\textsf{₹}\ 75000$
Total Amount returned (A) = $\textsf{₹}\ 80000$
Time Period = 1 year
To Find:
The interest paid.
Solution:
The total amount returned includes the principal amount that was borrowed and the interest accumulated over the given time period.
The relationship between Total Amount, Principal, and Interest is:
Total Amount = Principal + Interest
To find the interest, we can rearrange this equation:
Interest = Total Amount - Principal
Substitute the given values into the equation:
Interest = $\textsf{₹}\ 80000 - \textsf{₹}\ 75000$
Perform the subtraction:
Interest = $\textsf{₹}\ 5000$
The interest paid by John is $\textsf{₹}\ 5000$.
Example 10: If Meenakshee pays an interest of ₹ 1500 for 4 years on a sum of ₹ 2500, find the rate of interest per annum (p.a.)
Answer:
Given:
Simple Interest (SI) = $\textsf{₹}\ 1500$
Principal (P) = $\textsf{₹}\ 2500$
Time (T) = 4 years
To Find:
The rate of interest per annum (R).
Solution:
The formula for simple interest is given by:
$SI = \frac{P \times R \times T}{100}$
We are given SI, P, and T, and we need to find R. We can rearrange the formula to solve for R:
$R = \frac{SI \times 100}{P \times T}$
Now, substitute the given values into the formula:
$R = \frac{1500 \times 100}{2500 \times 4}$
Perform the calculation:
$R = \frac{150000}{10000}$
$R = \frac{\cancel{150000}}{\cancel{10000}}$
$R = 15$
The rate of interest per annum is 15%.
Answer: The rate of interest per annum is 15%.
Example 11: Refer to the graphic. If a cheetah and tortoise travel at their top speeds for 1minute; how much farther does the cheetah travel?
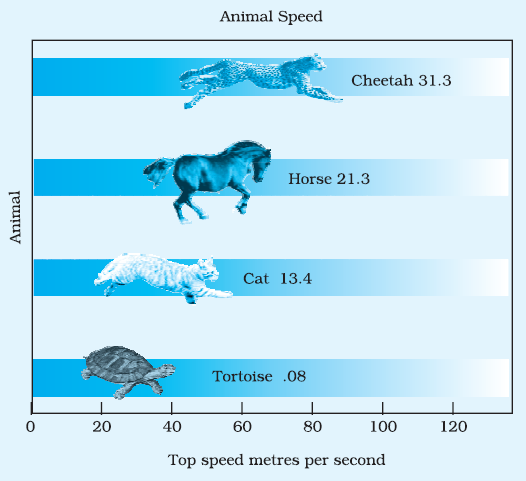
Answer:
Given:
Top speed of cheetah ($V_c$) = 60 mph
Top speed of tortoise ($V_t$) = 0.17 mph
Time of travel (T) = 1 minute
To Find:
How much farther does the cheetah travel than the tortoise in 1 minute.
Solution:
The speeds are given in miles per hour (mph), and the time is given in minutes. To calculate the distance travelled, we need to use consistent units. Let's convert the time from minutes to hours.
There are 60 minutes in 1 hour.
$T = 1 \text{ minute} = \frac{1}{60} \text{ hours}$
The formula for distance is: Distance = Speed $\times$ Time.
Calculate the distance travelled by the cheetah in 1 minute:
$D_c = V_c \times T$
$D_c = 60 \text{ mph} \times \frac{1}{60} \text{ hours}$
$D_c = \frac{60}{60}$ miles
$D_c = 1$ mile
Calculate the distance travelled by the tortoise in 1 minute:
$D_t = V_t \times T$
$D_t = 0.17 \text{ mph} \times \frac{1}{60} \text{ hours}$
$D_t = \frac{0.17}{60}$ miles
To find how much farther the cheetah travels, we subtract the distance travelled by the tortoise from the distance travelled by the cheetah:
Difference $= D_c - D_t$
Difference $= 1 \text{ mile} - \frac{0.17}{60} \text{ miles}$
Difference $= \frac{60}{60} - \frac{0.17}{60}$ miles
Difference $= \frac{60 - 0.17}{60}$ miles
Difference $= \frac{59.83}{60}$ miles
Now, calculate the decimal value:
$\frac{59.83}{60} \approx 0.997166...$
The cheetah travels approximately 0.997 miles farther than the tortoise in 1 minute.
Answer: The cheetah travels $\frac{59.83}{60}$ miles or approximately 0.997 miles farther.
Exercise
Question 1 to 23 (Multiple Choice Questions)
In questions 1 to 23, there are four options, out of which one is correct. write the correct one.
Question 1. 20% of 700 m is
(a) 560 m
(b) 70 m
(c) 210 m
(d) 140 m
Answer:
Solution:
To calculate 20% of 700 m, we convert the percentage to a fraction and multiply by 700 m.
$20\%$ of $700$ m $= \frac{20}{100} \times 700$ m
We can simplify the fraction or perform the multiplication directly.
$= \frac{\cancel{20}^{1}}{\cancel{100}_{5}} \times 700$ m
$= \frac{1}{5} \times 700$ m
$= \frac{\cancel{700}^{140}}{\cancel{5}_{1}}$ m
$= 140$ m
Comparing the result with the given options:
(a) 560 m
(b) 70 m
(c) 210 m
(d) 140 m
The calculated value, 140 m, matches option (d).
The correct answer is (d) 140 m.
Question 2. Gayatri’s income is ₹ 1,60,000 per year. She pays 15% of this as house rent and 10% of the remainder on her child’s education. The money left with her is
(a) ₹ 136000
(b) ₹ 120000
(c) ₹ 122400
(d) ₹ 14000
Answer:
Given:
Gayatri's annual income = $\textsf{₹} 1,60,000$
Percentage paid as house rent = $15\%$ of income
Percentage paid on child's education = $10\%$ of the remainder
To Find:
The money left with her.
Solution:
First, calculate the amount paid as house rent.
House rent = $15\%$ of $\textsf{₹} 1,60,000$
House rent = $\frac{15}{100} \times 160000$
House rent = $15 \times \frac{160000}{100}$
House rent = $15 \times 1600$
House rent = $\textsf{₹} 24,000$
Next, calculate the money remaining after paying house rent.
Money remaining = Total income - House rent
Money remaining = $\textsf{₹} 1,60,000 - \textsf{₹} 24,000$
Money remaining = $\textsf{₹} 136,000$
Now, calculate the amount paid on child's education, which is $10\%$ of the remainder.
Education expense = $10\%$ of $\textsf{₹} 136,000$
Education expense = $\frac{10}{100} \times 136000$
Education expense = $\frac{1}{10} \times 136000$
Education expense = $13600$
Education expense = $\textsf{₹} 13,600$
Finally, calculate the money left with her after paying for education.
Money left = Money remaining after rent - Education expense
Money left = $\textsf{₹} 136,000 - \textsf{₹} 13,600$
Money left = $\textsf{₹} 122,400$
Comparing the result with the given options, $\textsf{₹} 122,400$ matches option (c).
The correct answer is (c) $\textsf{₹} 122400$.
Question 3. The ratio of Fatima’s income to her savings is 4 : 1. The percentage of money saved by her is :
(a) 20%
(b) 25%
(c) 40%
(d) 80%
Answer:
Given:
Ratio of Fatima's income to her savings is $4 : 1$.
To Find:
The percentage of money saved by her.
Solution:
Let the income be represented by 4 parts and the savings be represented by 1 part.
Total income = 4 parts
Savings = 1 part
The total money (income) consists of the savings and the expenditure (money not saved).
The ratio of income to savings means that for every 4 units of income, 1 unit is saved.
The total number of parts representing the income is the sum of the ratio terms: $4 + 1 = 5$ parts.
However, the ratio $4:1$ is explicitly income:savings. So, the total income is represented by 4 parts, and savings by 1 part.
Percentage of money saved is calculated as (Savings / Income) $\times 100\%$.
Percentage Savings $= \frac{\text{Savings}}{\text{Income}} \times 100\%$
Using the ratio, Savings can be considered as 1 unit and Income as 4 units.
Percentage Savings $= \frac{1}{4} \times 100\%$
Percentage Savings $= \frac{100}{4} \%$
Percentage Savings $= 25\%$
Comparing the result with the given options:
(a) 20%
(b) 25%
(c) 40%
(d) 80%
The calculated percentage, 25%, matches option (b).
The correct answer is (b) 25%.
Question 4. 0.07 is equal to
(a) 70%
(b) 7%
(c) 0.7%
(d) 0.07%
Answer:
Solution:
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent symbol ($\%$).
We need to convert 0.07 to a percentage.
$0.07 \times 100\%$
Multiplying 0.07 by 100 gives:
$0.07 \times 100 = 7$
So, $0.07$ is equal to $7\%$.
Comparing the result with the given options:
(a) 70%
(b) 7%
(c) 0.7%
(d) 0.07%
The calculated value, 7%, matches option (b).
The correct answer is (b) 7%.
Question 5. In a scout camp, 40% of the scouts were from Gujarat State and 20% of these were from Ahmedabad. The percentage of scouts in the camp from Ahmedabad is:
(a) 25
(b) 32.5
(c) 8
(d) 50
Answer:
Given:
Percentage of scouts from Gujarat = $40\%$ of total scouts
Percentage of scouts from Ahmedabad = $20\%$ of scouts from Gujarat
To Find:
The percentage of scouts from Ahmedabad in the camp relative to the total number of scouts.
Solution:
Let the total number of scouts in the camp be $T$.
Number of scouts from Gujarat = $40\%$ of $T$
Scouts from Gujarat $= \frac{40}{100} \times T = 0.40T$
The scouts from Ahmedabad are $20\%$ of the scouts from Gujarat.
Number of scouts from Ahmedabad = $20\%$ of (Scouts from Gujarat)
Scouts from Ahmedabad $= 20\%$ of $(0.40T)$
Scouts from Ahmedabad $= \frac{20}{100} \times (0.40T)$
Scouts from Ahmedabad $= 0.20 \times 0.40T$
Scouts from Ahmedabad $= 0.08T$
To express this as a percentage of the total number of scouts ($T$), we multiply the decimal by 100.
Percentage of scouts from Ahmedabad $= 0.08 \times 100\%$
Percentage of scouts from Ahmedabad $= 8\%$
Comparing the result with the given options:
(a) 25
(b) 32.5
(c) 8
(d) 50
The calculated percentage, 8%, matches option (c).
The correct answer is (c) 8.
Question 6. What percent of ₹ 4500 is ₹ 9000?
(a) 200
(b) $\frac{1}{2}$
(c) 2
(d) 50
Answer:
Solution:
We need to find what percentage of $\textsf{₹} 4500$ is $\textsf{₹} 9000$.
Let the required percentage be $x\%$.
According to the question, $x\%$ of $\textsf{₹} 4500$ is $\textsf{₹} 9000$.
We can write this as an equation:
$\frac{x}{100} \times 4500 = 9000$
Now, we solve for $x$:
$x \times \frac{4500}{100} = 9000$
$x \times 45 = 9000$
$x = \frac{9000}{45}$
Performing the division:
$x = \frac{\cancel{9000}^{200}}{\cancel{45}_{1}}$
$x = 200$
So, 200% of $\textsf{₹} 4500$ is $\textsf{₹} 9000$. The question asks for the percentage value, which is 200.
Comparing the result with the given options:
(a) 200
(b) $\frac{1}{2}$
(c) 2
(d) 50
The calculated value, 200, matches option (a).
The correct answer is (a) 200.
Question 7. 5.2 is equal to
(a) 52%
(b) 5.2%
(c) 520%
(d) 0.52%
Answer:
Solution:
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent symbol ($\%$).
We need to convert 5.2 to a percentage.
$5.2 \times 100\%$
Multiplying 5.2 by 100 gives:
$5.2 \times 100 = 520$
So, $5.2$ is equal to $520\%$.
Comparing the result with the given options:
(a) 52%
(b) 5.2%
(c) 520%
(d) 0.52%
The calculated value, 520%, matches option (c).
The correct answer is (c) 520%.
Question 8. The ratio 3 : 8 is equal to
(a) 3.75%
(b) 37.5%
(c) 0.375%
(d) 267%
Answer:
Solution:
A ratio $a : b$ can be written as a fraction $\frac{a}{b}$.
So, the ratio $3 : 8$ can be written as the fraction $\frac{3}{8}$.
To convert a fraction to a percentage, we multiply the fraction by 100 and add the percent symbol ($\%$).
Percentage $= \frac{3}{8} \times 100\%$
Percentage $= \frac{300}{8} \%$
Now, we perform the division $\frac{300}{8}$:
$\frac{300}{8} = \frac{\cancel{300}^{75}}{\cancel{8}_{2}}$ (dividing numerator and denominator by 4)
$= \frac{75}{2}$
$= 37.5$
So, $\frac{3}{8}$ is equal to $37.5\%$.
Comparing the result with the given options:
(a) 3.75%
(b) 37.5%
(c) 0.375%
(d) 267%
The calculated percentage, 37.5%, matches option (b).
The correct answer is (b) 37.5%.
Question 9. 225% is equal to
(a) 9 : 4
(b) 4 : 9
(c) 3 : 2
(d) 2 : 3
Answer:
Solution:
To convert a percentage to a fraction, we divide the percentage value by 100.
$225\% = \frac{225}{100}$
Now, we simplify the fraction $\frac{225}{100}$ to its lowest terms by finding the greatest common divisor (GCD) of 225 and 100.
Both numbers are divisible by 5.
$\frac{\cancel{225}^{45}}{\cancel{100}_{20}}$
The fraction is now $\frac{45}{20}$. Both numbers are still divisible by 5.
$\frac{\cancel{45}^{9}}{\cancel{20}_{4}}$
The simplified fraction is $\frac{9}{4}$.
A fraction $\frac{a}{b}$ can be expressed as a ratio $a : b$.
So, the fraction $\frac{9}{4}$ is equal to the ratio $9 : 4$.
Comparing the result with the given options:
(a) 9 : 4
(b) 4 : 9
(c) 3 : 2
(d) 2 : 3
The calculated ratio, 9 : 4, matches option (a).
The correct answer is (a) 9 : 4.
Question 10. A bicycle is purchased for ₹ 1800 and is sold at a profit of 12%. Its selling price is
(a) ₹ 1584
(b) ₹ 2016
(c) ₹ 1788
(d) ₹ 1812
Answer:
Given:
Cost Price (CP) of bicycle = $\textsf{₹} 1800$
Profit percentage = $12\%$
To Find:
Selling Price (SP) of the bicycle.
Solution:
The profit amount is calculated based on the cost price and the profit percentage.
Profit amount = Profit percentage $\times$ CP
Profit amount $= 12\%$ of $\textsf{₹} 1800$
Profit amount $= \frac{12}{100} \times 1800$
Profit amount $= 12 \times \frac{\cancel{1800}^{18}}{\cancel{100}_{1}}$
Profit amount $= 12 \times 18$
Let's calculate $12 \times 18$ using multiplication:
$\begin{array}{cc}& & 1 & 8 \\ \times & & 1 & 2 \\ \hline && 3 & 6 \\ & 1 & 8 & \times \\ \hline & 2 & 1 & 6 \\ \hline \end{array}$Profit amount $= \textsf{₹} 216$
The selling price is the sum of the cost price and the profit amount.
SP = CP + Profit amount
SP $= \textsf{₹} 1800 + \textsf{₹} 216$
SP $= \textsf{₹} 2016$
Comparing the result with the given options:
(a) ₹ 1584
(b) ₹ 2016
(c) ₹ 1788
(d) ₹ 1812
The calculated selling price, $\textsf{₹} 2016$, matches option (b).
The correct answer is (b) $\textsf{₹} 2016$.
Question 11. A cricket bat was purchased for ₹ 800 and was sold for ₹ 1600. Then profit earned is
(a) 100%
(b) 64%
(c) 50%
(d) 60%
Answer:
Given:
Cost Price (CP) of cricket bat = $\textsf{₹} 800$
Selling Price (SP) of cricket bat = $\textsf{₹} 1600$
To Find:
Profit percentage earned.
Solution:
Since the Selling Price is greater than the Cost Price ($\textsf{₹} 1600 > \textsf{₹} 800$), there is a profit.
Profit amount = SP - CP
Profit amount $= \textsf{₹} 1600 - \textsf{₹} 800$
Profit amount $= \textsf{₹} 800$
The profit percentage is calculated as the ratio of the profit amount to the Cost Price, multiplied by 100.
Profit Percentage $= \frac{\text{Profit amount}}{\text{CP}} \times 100\%$
Profit Percentage $= \frac{800}{800} \times 100\%$
Profit Percentage $= 1 \times 100\%$
Profit Percentage $= 100\%$
Comparing the result with the given options:
(a) 100%
(b) 64%
(c) 50%
(d) 60%
The calculated profit percentage, 100%, matches option (a).
The correct answer is (a) 100%.
Question 12. A farmer bought a buffalo for ₹ 44000 and a cow for ₹ 18000. He sold the buffalo at a loss of 5% but made a profit of 10% on the cow. The net result of the transaction is
(a) loss of ₹ 200
(b) profit of ₹ 400
(c) loss of ₹ 400
(d) profit of ₹ 200
Answer:
Given:
CP of buffalo = $\textsf{₹} 44000$, Loss % on buffalo = $5\%$
CP of cow = $\textsf{₹} 18000$, Profit % on cow = $10\%$
To Find:
The net result (profit or loss) from the whole transaction.
Solution:
Calculate the loss amount on the buffalo:
Loss = $5\%$ of CP of buffalo
Loss $= \frac{5}{100} \times 44000$
Loss $= 5 \times \frac{44000}{100}$
Loss $= 5 \times 440$
Loss $= \textsf{₹} 2200$
Calculate the profit amount on the cow:
Profit = $10\%$ of CP of cow
Profit $= \frac{10}{100} \times 18000$
Profit $= 10 \times \frac{18000}{100}$
Profit $= 10 \times 180$
Profit $= \textsf{₹} 1800$
Now, find the net result of the transaction by comparing the total profit and total loss amounts.
Total Profit $= \textsf{₹} 1800$ (from cow)
Total Loss $= \textsf{₹} 2200$ (from buffalo)
Since Total Loss $>$ Total Profit, there is a net loss.
Net Loss = Total Loss - Total Profit
Net Loss $= \textsf{₹} 2200 - \textsf{₹} 1800$
Net Loss $= \textsf{₹} 400$
The net result of the transaction is a loss of $\textsf{₹} 400$.
Comparing the result with the given options, a loss of $\textsf{₹} 400$ matches option (c).
The correct answer is (c) loss of ₹ 400.
Question 13. If Mohan’s income is 25% more than Raman’s income, then Raman’s income is less than Mohan’s income by
(a) 25%
(b) 80%
(c) 20%
(d) 75%
Answer:
Given:
Mohan's income is $25\%$ more than Raman's income.
To Find:
The percentage by which Raman's income is less than Mohan's income.
Solution:
Let's assume Raman's income to be $\textsf{₹} 100$ for simplicity.
Raman's income $= \textsf{₹} 100$
Mohan's income is $25\%$ more than Raman's income.
Amount of increase $= 25\%$ of $\textsf{₹} 100$
Amount of increase $= \frac{25}{100} \times 100 = \textsf{₹} 25$
Mohan's income $=$ Raman's income $+$ Amount of increase
Mohan's income $= \textsf{₹} 100 + \textsf{₹} 25 = \textsf{₹} 125$
Now, we need to find by what percentage Raman's income ($\textsf{₹} 100$) is less than Mohan's income ($\textsf{₹} 125$).
The difference between Mohan's income and Raman's income is:
Difference $= \textsf{₹} 125 - \textsf{₹} 100 = \textsf{₹} 25$
To find the percentage by which Raman's income is less than Mohan's income, we calculate the difference as a percentage of Mohan's income.
Percentage less $= \frac{\text{Difference}}{\text{Mohan's Income}} \times 100\%$
Percentage less $= \frac{25}{125} \times 100\%$
Percentage less $= \frac{\cancel{25}^{1}}{\cancel{125}_{5}} \times 100\%$
Percentage less $= \frac{1}{5} \times 100\%$
Percentage less $= \frac{100}{5}\%$
Percentage less $= 20\%$
So, Raman's income is $20\%$ less than Mohan's income.
Comparing the result with the given options:
(a) 25%
(b) 80%
(c) 20%
(d) 75%
The calculated percentage, 20%, matches option (c).
The correct answer is (c) 20%.
Question 14. The interest on ₹ 30000 for 3 years at the rate of 15% per annum is
(a) ₹ 4500
(b) ₹ 9000
(c) ₹ 18000
(d) ₹ 13500
Answer:
Given:
Principal (P) = $\textsf{₹} 30000$
Time (T) = 3 years
Rate of Interest (R) = $15\%$ per annum
To Find:
The simple interest (SI).
Solution:
The formula for calculating Simple Interest is:
$SI = \frac{P \times R \times T}{100}$
Substitute the given values into the formula:
$SI = \frac{30000 \times 15 \times 3}{100}$
Simplify the expression:
$SI = 300 \times 15 \times 3$
$SI = 300 \times (15 \times 3)$
$SI = 300 \times 45$
Perform the multiplication:
$300 \times 45 = 3 \times 100 \times 45$
$= 3 \times 4500$
$= 13500$
So, the Simple Interest is $\textsf{₹} 13500$.
Comparing the result with the given options:
(a) ₹ 4500
(b) ₹ 9000
(c) ₹ 18000
(d) ₹ 13500
The calculated interest, $\textsf{₹} 13500$, matches option (d).
The correct answer is (d) $\textsf{₹} 13500$.
Question 15. Amount received on ₹ 3000 for 2 years at the rate of 11% per annum is
(a) ₹ 2340
(b) ₹ 3660
(c) ₹ 4320
(d) ₹ 3330
Answer:
Given:
Principal (P) = $\textsf{₹} 3000$
Time (T) = 2 years
Rate of Interest (R) = $11\%$ per annum
To Find:
The amount received.
Solution:
First, we need to calculate the Simple Interest (SI).
The formula for Simple Interest is:
$SI = \frac{P \times R \times T}{100}$
Substitute the given values into the formula:
$SI = \frac{3000 \times 11 \times 2}{100}$
Simplify the expression:
$SI = 30 \times 11 \times 2$
$SI = 30 \times 22$
$SI = 660$
So, the Simple Interest is $\textsf{₹} 660$.
The amount received is the sum of the Principal and the Simple Interest.
Amount = Principal + SI
Amount $= \textsf{₹} 3000 + \textsf{₹} 660$
Amount $= \textsf{₹} 3660$
Comparing the result with the given options:
(a) ₹ 2340
(b) ₹ 3660
(c) ₹ 4320
(d) ₹ 3330
The calculated amount, $\textsf{₹} 3660$, matches option (b).
The correct answer is (b) $\textsf{₹} 3660$.
Question 16. Interest on ₹ 12000 for 1 month at the rate of 10 % per annum is
(a) ₹ 1200
(b) ₹ 600
(c) ₹ 100
(d) ₹ 12100
Answer:
Given:
Principal (P) = $\textsf{₹} 12000$
Time (T) = 1 month
Rate of Interest (R) = $10\%$ per annum
To Find:
The simple interest (SI) for 1 month.
Solution:
The rate of interest is given per annum, so we need to express the time in years.
1 year = 12 months
So, 1 month = $\frac{1}{12}$ years.
Time (T) = $\frac{1}{12}$ years.
The formula for calculating Simple Interest is:
$SI = \frac{P \times R \times T}{100}$
Substitute the given values into the formula:
$SI = \frac{12000 \times 10 \times \frac{1}{12}}{100}$
Simplify the expression:
$SI = \frac{12000 \times 10}{100 \times 12}$
$SI = \frac{120000}{1200}$
$SI = \frac{\cancel{120000}^{100}}{\cancel{1200}_{1}}$
$SI = 100$
So, the Simple Interest is $\textsf{₹} 100$.
Comparing the result with the given options:
(a) ₹ 1200
(b) ₹ 600
(c) ₹ 100
(d) ₹ 12100
The calculated interest, $\textsf{₹} 100$, matches option (c).
The correct answer is (c) $\textsf{₹} 100$.
Question 17. Rajni and Mohini deposited ₹ 3000 and ₹ 4000 in a company at the rate of 10% per annum for 3 years and $2\frac{1}{2}$ years respectively. The difference of the amounts received by them will be
(a) ₹ 100
(b) ₹ 1000
(c) ₹ 900
(d) ₹ 1100
Answer:
Given:
For Rajni:
Principal ($P_R$) = $\textsf{₹} 3000$
Time ($T_R$) = 3 years
Rate of Interest (R) = $10\%$ per annum
For Mohini:
Principal ($P_M$) = $\textsf{₹} 4000$
Time ($T_M$) = $2\frac{1}{2}$ years = 2.5 years
Rate of Interest (R) = $10\%$ per annum
To Find:
The difference of the amounts received by them.
Solution:
First, calculate the Simple Interest ($SI_R$) for Rajni.
$SI_R = \frac{P_R \times R \times T_R}{100}$
$SI_R = \frac{3000 \times 10 \times 3}{100}$
$SI_R = \frac{30000 \times 3}{100}$
$SI_R = 300 \times 3 = \textsf{₹} 900$
Now, calculate the Amount ($A_R$) received by Rajni.
$A_R = P_R + SI_R$
$A_R = \textsf{₹} 3000 + \textsf{₹} 900 = \textsf{₹} 3900$
Next, calculate the Simple Interest ($SI_M$) for Mohini.
$SI_M = \frac{P_M \times R \times T_M}{100}$
$SI_M = \frac{4000 \times 10 \times 2.5}{100}$
$SI_M = \frac{40000 \times 2.5}{100}$
$SI_M = 400 \times 2.5 = \textsf{₹} 1000$
Now, calculate the Amount ($A_M$) received by Mohini.
$A_M = P_M + SI_M$
$A_M = \textsf{₹} 4000 + \textsf{₹} 1000 = \textsf{₹} 5000$
Finally, find the difference between the amounts received by them.
Difference $= A_M - A_R$
Difference $= \textsf{₹} 5000 - \textsf{₹} 3900$
Difference $= \textsf{₹} 1100$
The difference of the amounts received is $\textsf{₹} 1100$.
Comparing the result with the given options:
(a) ₹ 100
(b) ₹ 1000
(c) ₹ 900
(d) ₹ 1100
The calculated difference, $\textsf{₹} 1100$, matches option (d).
The correct answer is (d) $\textsf{₹} 1100$.
Question 18. If 90% of x is 315 km, then the value of x is
(a) 325 km
(b) 350 km
(c) 405 km
(d) 340 km
Answer:
Given:
$90\%$ of $x$ is 315 km.
To Find:
The value of $x$.
Solution:
We can write the given information as an equation:
$90\%$ of $x = 315$
Convert the percentage to a fraction:
$\frac{90}{100} \times x = 315$
Simplify the fraction $\frac{90}{100}$:
$\frac{\cancel{90}^{9}}{\cancel{100}_{10}} \times x = 315$
$\frac{9}{10} \times x = 315$
Now, solve for $x$. Multiply both sides of the equation by $\frac{10}{9}$ (the reciprocal of $\frac{9}{10}$).
$x = 315 \times \frac{10}{9}$
Simplify the expression:
$x = \frac{\cancel{315}^{35} \times 10}{\cancel{9}_{1}}$ (since $315 \div 9 = 35$)
$x = 35 \times 10$
$x = 350$
Since the unit given in the question is km, the value of $x$ is 350 km.
Comparing the result with the given options:
(a) 325 km
(b) 350 km
(c) 405 km
(d) 340 km
The calculated value, 350 km, matches option (b).
The correct answer is (b) 350 km.
Question 19. On selling an article for ₹ 329, a dealer lost 6%. The cost price of the article is
(a) ₹ 310.37
(b) ₹ 348.74
(c) ₹ 335
(d) ₹ 350
Answer:
Given:
Selling Price (SP) = $\textsf{₹} 329$
Loss percentage = $6\%$
To Find:
The Cost Price (CP) of the article.
Solution:
When there is a loss, the selling price is calculated as:
$SP = CP - \text{Loss amount}$
The loss amount is the loss percentage of the Cost Price:
Loss amount $= \text{Loss \%} \times CP$
Loss amount $= \frac{6}{100} \times CP = 0.06 \times CP$
Substitute the loss amount into the SP formula:
$SP = CP - 0.06 \times CP$
$SP = CP (1 - 0.06)$
$SP = CP (0.94)$
We are given the SP, so we can write the equation:
$329 = CP \times 0.94$
To find CP, divide the SP by 0.94:
$CP = \frac{329}{0.94}$
To perform the division, we can multiply the numerator and denominator by 100 to remove the decimal:
$CP = \frac{329 \times 100}{0.94 \times 100} = \frac{32900}{94}$
Perform the long division:
$\begin{array}{r} 350\phantom{)} \\ 94{\overline{\smash{\big)}\,32900\phantom{)}}} \\ \underline{-~\phantom{(}282\phantom{00)}} \\ 0470\phantom{0)} \\ \underline{-~\phantom{()}470\phantom{0)}} \\ 0000\phantom{)} \\ \underline{-~\phantom{()...}0} \\ 0 \end{array}$
So, $CP = 350$.
The cost price of the article is $\textsf{₹} 350$.
Alternatively, using a direct formula:
When there is a loss, $SP = CP \times \frac{(100 - \text{Loss \%})}{100}$
$329 = CP \times \frac{(100 - 6)}{100}$
$329 = CP \times \frac{94}{100}$
$329 = CP \times 0.94$
$CP = \frac{329}{0.94} = \frac{32900}{94} = 350$
The cost price is $\textsf{₹} 350$.
Comparing the result with the given options:
(a) ₹ 310.37
(b) ₹ 348.74
(c) ₹ 335
(d) ₹ 350
The calculated cost price, $\textsf{₹} 350$, matches option (d).
The correct answer is (d) $\textsf{₹} 350$.
Question 20. $\frac{25\% \;of \;50\% \;of \;100\%}{25 \;×\; 50}$ is equal to
(a) 1.1%
(b) 0.1%
(c) 0.01%
(d) 1 %
Answer:
Solution:
We need to evaluate the given expression: $\frac{25\% \;of \;50\% \;of \;100\%}{25 \;×\; 50}$
Recall that "of" means multiplication and a percentage $p\%$ can be written as $\frac{p}{100}$.
Let's evaluate the numerator first:
Numerator = $25\% \;of \;50\% \;of \;100\%$
= $\frac{25}{100} \times \frac{50}{100} \times \frac{100}{100}$
= $\frac{25}{100} \times \frac{50}{100} \times 1$
= $\frac{25}{100} \times \frac{50}{100}$
= $\frac{25 \times 50}{100 \times 100}$
= $\frac{1250}{10000}$
Now, evaluate the denominator:
Denominator = $25 \times 50 = 1250$
Now, put the numerator and denominator back into the expression:
Expression $= \frac{\frac{1250}{10000}}{1250}$
$= \frac{1250}{10000} \div 1250$
$= \frac{1250}{10000} \times \frac{1}{1250}$
$= \frac{\cancel{1250}}{\cancel{10000}_{10000/10000=1} \times 1250} \times \frac{1}{\cancel{1250}}$
$= \frac{1}{10000}$
The value of the expression is $\frac{1}{10000}$.
We need to express this as a percentage. To convert a fraction to a percentage, multiply by 100%.
Percentage $= \frac{1}{10000} \times 100\%$
$= \frac{100}{10000} \%$
$= \frac{\cancel{100}^{1}}{\cancel{10000}_{100}} \%$
$= \frac{1}{100} \%$
$= 0.01\%$
Comparing the result with the given options:
(a) 1.1%
(b) 0.1%
(c) 0.01%
(d) 1 %
The calculated value, 0.01%, matches option (c).
The correct answer is (c) 0.01%.
Question 21. The sum which will earn a simple interest of ₹ 126 in 2 years at 14% per annum is
(a) ₹ 394
(b) ₹ 395
(c) ₹ 450
(d) ₹ 540
Answer:
Given:
Simple Interest (SI) = $\textsf{₹} 126$
Time (T) = 2 years
Rate of Interest (R) = $14\%$ per annum
To Find:
The principal sum (P).
Solution:
The formula for Simple Interest is:
$SI = \frac{P \times R \times T}{100}$
We need to find P. We can rearrange the formula to solve for P:
$P = \frac{SI \times 100}{R \times T}$
Substitute the given values into the formula:
$P = \frac{126 \times 100}{14 \times 2}$
Simplify the denominator:
$P = \frac{126 \times 100}{28}$
Simplify the expression. We can divide 100 by 28 or 126 by 14 or 28.
$P = \frac{126}{28} \times 100$
Divide 126 by 14:
$P = \frac{\cancel{126}^{9}}{\cancel{28}_{2}} \times 100$ (since $126 \div 14 = 9$ and $28 \div 14 = 2$)
$P = \frac{9}{2} \times 100$
$P = 9 \times \frac{100}{2}$
$P = 9 \times 50$
$P = 450$
So, the principal sum is $\textsf{₹} 450$.
Comparing the result with the given options:
(a) ₹ 394
(b) ₹ 395
(c) ₹ 450
(d) ₹ 540
The calculated principal, $\textsf{₹} 450$, matches option (c).
The correct answer is (c) $\textsf{₹} 450$.
Question 22. The per cent that represents the unshaded region in the figure.

(a) 75%
(b) 50%
(c) 40%
(d) 60%
Answer:
Solution:
Let's examine the provided figure. The figure appears to be a square divided into smaller equal parts. By carefully observing the figure, we can count the total number of equal parts and the number of unshaded parts.
Total number of equal parts in the figure is 5.
Number of unshaded parts is 3.
Number of shaded parts is 2.
The fraction that represents the unshaded region is:
Fraction of unshaded region $= \frac{\text{Number of unshaded parts}}{\text{Total number of parts}}$
Fraction of unshaded region $= \frac{3}{5}$
To express this fraction as a percentage, we multiply the fraction by 100%.
Percentage of unshaded region $= \frac{3}{5} \times 100\%$
Percentage of unshaded region $= \frac{3 \times 100}{5} \%$
Percentage of unshaded region $= \frac{300}{5} \%$
Percentage of unshaded region $= 60\%$
Comparing the result with the given options:
(a) 75%
(b) 50%
(c) 40%
(d) 60%
The calculated percentage of the unshaded region, 60%, matches option (d).
The correct answer is (d) 60%.
Question 23. The per cent that represents the shaded region in the figure is

(a) 36%
(b) 64%
(c) 27%
(d) 48%
Answer:
Solution:
To find the percentage that represents the shaded region, we need to determine the fraction of the figure that is shaded and then convert that fraction to a percentage.
Upon examining the figure, we count the total number of equal small squares that make up the figure.
Total number of equal small squares = 100
Next, we count the number of these small squares that are shaded.
Number of shaded squares = 36
The fraction of the figure that is shaded is the ratio of the number of shaded squares to the total number of squares.
Fraction of shaded region $= \frac{\text{Number of shaded squares}}{\text{Total number of squares}} = \frac{36}{100}$
To convert this fraction to a percentage, we multiply by 100%.
Percentage of shaded region $= \frac{36}{100} \times 100\%$
Percentage of shaded region $= 36\%$
Comparing the result with the given options:
(a) 36%
(b) 64%
(c) 27%
(d) 48%
The calculated percentage, 36%, matches option (a).
The correct answer is (a) 36%.
Question 24 to 59 (Fill in the Blanks)
In each of the questions 24 to 59, fill in the blanks to make the statements true.
Question 24. 2 : 3 = ________ %
Answer:
To convert a ratio to a percentage, we first write the ratio as a fraction.
The given ratio is 2 : 3.
We can write this ratio as a fraction:
$2 : 3 = \frac{2}{3}$
To convert a fraction to a percentage, we multiply the fraction by 100%.
So, we need to calculate $\frac{2}{3} \times 100\%$.
Calculation:
$\frac{2}{3} \times 100\% = \frac{2 \times 100}{3}\%$
$= \frac{200}{3}\%$
We can express $\frac{200}{3}$ as a mixed number or a decimal percentage.
As a mixed number:
When 200 is divided by 3, the quotient is 66 and the remainder is 2.
So, $\frac{200}{3} = 66 \frac{2}{3}$.
Thus, $\frac{200}{3}\% = 66 \frac{2}{3}\%$.
As a decimal percentage:
$\frac{2}{3} = 0.666... = 0.\overline{6}$
So, $\frac{2}{3} \times 100\% = 0.\overline{6} \times 100\% = 66.\overline{6}\%$.
Both $66 \frac{2}{3}\%$ and $66.\overline{6}\%$ are correct representations of the percentage.
Therefore, 2 : 3 = $66 \frac{2}{3}\%$ or $66.\overline{6}\%$.
The blank can be filled with either value depending on the required format. Assuming an exact value is preferred, the mixed number form is suitable.
The final answer is $66 \frac{2}{3}$.
Question 25. $18\frac{3}{4}$ % = _______ : _______
Answer:
To convert a percentage to a ratio, we first convert the percentage into a fraction and then simplify it to its lowest terms.
The given percentage is $18\frac{3}{4}\%$.
First, convert the mixed number to an improper fraction:
$18\frac{3}{4} = \frac{(18 \times 4) + 3}{4} = \frac{72 + 3}{4} = \frac{75}{4}$.
So, we have $\frac{75}{4}\%$.
To convert a percentage to a fraction, we divide by 100.
$18\frac{3}{4}\% = \frac{\frac{75}{4}}{100}$
$= \frac{75}{4 \times 100} = \frac{75}{400}$
Now, we need to simplify the fraction $\frac{75}{400}$ to its lowest terms.
We can find the greatest common divisor (GCD) of 75 and 400.
Both 75 and 400 are divisible by 25.
$75 \div 25 = 3$
$400 \div 25 = 16$
So, the simplified fraction is $\frac{3}{16}$.
We can cancel the fraction as follows:
$\frac{\cancel{75}^{3}}{\cancel{400}_{16}} = \frac{3}{16}$
Finally, we write the simplified fraction as a ratio.
The fraction $\frac{3}{16}$ corresponds to the ratio 3 : 16.
Therefore, $18\frac{3}{4}\%$ = 3 : 16.
The blanks should be filled with 3 and 16 respectively.
Question 26. 30% of ₹ 360 = ________.
Answer:
To find a percentage of a quantity, we convert the percentage into a fraction or a decimal and then multiply it by the quantity.
The percentage is 30% and the quantity is ₹ 360.
We can write 30% as the fraction $\frac{30}{100}$.
So, 30% of ₹ 360 means $\frac{30}{100} \times \textsf{₹} \, 360$.
Let's calculate the value:
$ \frac{30}{100} \times 360 $
We can simplify the fraction by dividing both the numerator and the denominator by 10:
$ \frac{\cancel{30}^{3}}{\cancel{100}_{10}} \times 360 = \frac{3}{10} \times 360 $
Now, we can divide 360 by 10:
$ \frac{3}{10} \times \cancel{360}^{36} = 3 \times 36 $
Finally, multiply 3 by 36:
$3 \times 36 = 108$
Alternatively, using decimals:
30% = 0.30
0.30 $\times$ 360 = 108
The result is 108.
Since the original quantity was in Rupees, the result is also in Rupees.
So, 30% of ₹ 360 = ₹ 108.
The blank should be filled with ₹ 108.
Question 27. 120% of 50 km = ________.
Answer:
To find a percentage of a quantity, we convert the percentage into a fraction or a decimal and then multiply it by the quantity.
The percentage is 120% and the quantity is 50 km.
We can write 120% as the fraction $\frac{120}{100}$.
So, 120% of 50 km means $\frac{120}{100} \times 50 \, \text{km}$.
Let's calculate the value:
$ \frac{120}{100} \times 50 $
We can simplify the fraction and multiply:
$ \frac{120}{100} \times 50 = \frac{120}{\cancel{100}^{2}} \times \cancel{50}^{1} = \frac{120}{2} $
$ \frac{120}{2} = 60 $
Alternatively, using decimals:
120% = 1.20
$1.20 \times 50 = 60$
The result is 60.
Since the original quantity was in kilometers, the result is also in kilometers.
So, 120% of 50 km = 60 km.
The blank should be filled with 60 km.
Question 28. 2.5 = ________%
Answer:
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent symbol.
The given decimal is 2.5.
Multiply 2.5 by 100:
$2.5 \times 100 = 250$
Add the percent symbol to the result.
So, 2.5 expressed as a percentage is 250%.
Therefore, 2.5 = 250%.
Question 29. $\frac{8}{5}$ = _______ %
Answer:
To convert a fraction to a percentage, we multiply the fraction by 100%.
The given fraction is $\frac{8}{5}$.
We need to calculate $\frac{8}{5} \times 100\%$.
Calculate the value:
$ \frac{8}{5} \times 100\% = \frac{8 \times \cancel{100}^{20}}{\cancel{5}^{1}}\% $
$ = 8 \times 20\% $
$ = 160\% $
Alternatively, convert the fraction to a decimal first:
$\frac{8}{5} = 1.6$
Now convert the decimal to a percentage by multiplying by 100:
$1.6 \times 100\% = 160\%$
Therefore, $\frac{8}{5}$ = 160 %.
Question 30. A _______ with its denominator 100 is called a per cent.
Answer:
The question asks to complete the definition of a per cent.
By definition, a percentage is a way of expressing a number as a fraction of 100.
A quantity expressed as 'n per cent' (n%) means $\frac{n}{100}$. This is a fraction with a denominator of 100.
Therefore, a fraction with its denominator 100 is called a per cent.
The blank should be filled with the word fraction.
A fraction with its denominator 100 is called a per cent.
Question 31. 15 kg is _______ % of 50 kg.
Answer:
To find what percentage one quantity is of another, we write the first quantity as a fraction of the second quantity and then convert the fraction to a percentage.
We want to find what percentage 15 kg is of 50 kg.
We form the fraction: $\frac{\text{Part}}{\text{Whole}} = \frac{15 \, \text{kg}}{50 \, \text{kg}}$.
The units (kg) cancel out, leaving the fraction $\frac{15}{50}$.
Now, convert the fraction $\frac{15}{50}$ to a percentage by multiplying by 100%:
$ \frac{15}{50} \times 100\% $
Calculate the value:
$ \frac{15}{\cancel{50}^{1}} \times \cancel{100}^{2}\% = 15 \times 2\% $
$ = 30\% $
Alternatively, using decimals:
Convert the fraction to a decimal: $\frac{15}{50} = 0.3$
Convert the decimal to a percentage by multiplying by 100: $0.3 \times 100\% = 30\%$
So, 15 kg is 30% of 50 kg.
The blank should be filled with 30.
Question 32. Weight of Nikhil increased from 60 kg to 66 kg. Then, the increase in weight is _______ %.
Answer:
To find the percentage increase in weight, we first need to calculate the amount of increase and then express this increase as a percentage of the original weight.
Original weight = 60 kg
New weight = 66 kg
Increase in weight = New weight - Original weight
$= 66 \, \text{kg} - 60 \, \text{kg} = 6 \, \text{kg}$.
Now, we need to find the percentage increase.
Percentage Increase $= \frac{\text{Increase in weight}}{\text{Original weight}} \times 100\%$.
Percentage Increase $= \frac{6 \, \text{kg}}{60 \, \text{kg}} \times 100\%$.
Calculate the value:
$ \frac{6}{60} \times 100\% $
$ \frac{\cancel{6}^{1}}{\cancel{60}_{10}} \times 100\% = \frac{1}{10} \times 100\% $
$ \frac{1}{10} \times \cancel{100}^{10}\% = 1 \times 10\% $
$ = 10\% $
So, the increase in weight is 10%.
The blank should be filled with 10.
Question 33. In a class of 50 students, 8 % were absent on one day. The number of students present on that day was ________.
Answer:
We are given the total number of students and the percentage of students absent.
Total number of students = 50
Percentage of students absent = 8%
First, we need to find the number of students who were absent.
Number of absent students = 8% of 50.
This can be calculated as:
$8\% \text{ of } 50 = \frac{8}{100} \times 50$
Calculate the value:
$ \frac{8}{100} \times 50 = \frac{8}{\cancel{100}^{2}} \times \cancel{50}^{1} = \frac{8}{2} = 4 $
So, the number of absent students was 4.
To find the number of students present, we subtract the number of absent students from the total number of students.
Number of students present = Total students - Number of absent students
$= 50 - 4 = 46$
Alternatively, we can find the percentage of students present first.
Percentage of students present = 100% - Percentage of students absent
$= 100\% - 8\% = 92\%$.
Now, find 92% of the total number of students (50).
Number of students present = 92% of 50
$= \frac{92}{100} \times 50$
$= \frac{92}{\cancel{100}^{2}} \times \cancel{50}^{1} = \frac{92}{2} = 46$
In both methods, the number of students present is 46.
The blank should be filled with 46.
Question 34. Savitri obtained 440 marks out of 500 in an examination. She secured _______ % marks in the examination.
Answer:
To find the percentage of marks secured, we need to express the marks obtained as a fraction of the total marks and then convert this fraction into a percentage.
Marks obtained = 440
Total marks = 500
The fraction of marks obtained is $\frac{\text{Marks obtained}}{\text{Total marks}} = \frac{440}{500}$.
To convert this fraction to a percentage, we multiply by 100%:
Percentage secured $= \frac{440}{500} \times 100\%$.
Calculate the value:
$ \frac{440}{500} \times 100\% = \frac{440}{\cancel{500}_{5}} \times \cancel{100}^{1}\% $
$ = \frac{440}{5}\% $
Divide 440 by 5:
$ \frac{440}{5} = 88 $
So, the percentage secured is 88%.
Therefore, Savitri secured 88 % marks in the examination.
Question 35. Out of a total deposit of ₹ 1500 in her bank account, Abida withdrew 40% of the deposit. Now the balance in her account is ______.
Answer:
We are given the total deposit and the percentage of deposit withdrawn.
Total deposit = ₹ 1500
Percentage withdrawn = 40%
First, we need to find the amount of money withdrawn.
Amount withdrawn = 40% of ₹ 1500.
This can be calculated as:
$40\% \text{ of } \textsf{₹} \, 1500 = \frac{40}{100} \times 1500$
Calculate the value:
$ \frac{40}{100} \times 1500 = \frac{40}{\cancel{100}^{1}} \times \cancel{1500}^{15} = 40 \times 15 $
$40 \times 15 = 600$
So, the amount withdrawn is ₹ 600.
To find the balance in her account, we subtract the amount withdrawn from the total deposit.
Balance = Total deposit - Amount withdrawn
$= \textsf{₹} \, 1500 - \textsf{₹} \, 600 = \textsf{₹} \, 900$
Alternatively, we can find the percentage of the balance first.
Percentage balance = 100% - Percentage withdrawn
$= 100\% - 40\% = 60\%$.
Now, find 60% of the total deposit (₹ 1500).
Balance = 60% of ₹ 1500
$= \frac{60}{100} \times 1500$
$= \frac{60}{\cancel{100}^{1}} \times \cancel{1500}^{15} = 60 \times 15 = 900$
In both methods, the balance in her account is ₹ 900.
The blank should be filled with ₹ 900.
Question 36. ________ is 50% more than 60.
Answer:
We need to find a number that is 50% more than 60.
First, calculate 50% of 60.
$50\% \text{ of } 60 = \frac{50}{100} \times 60$
Calculate the value:
$ \frac{50}{100} \times 60 = \frac{\cancel{50}^{1}}{\cancel{100}_{2}} \times 60 = \frac{1}{2} \times 60 $
$ \frac{1}{2} \times 60 = 30 $
So, 50% of 60 is 30.
The number that is 50% more than 60 is obtained by adding this calculated value to 60.
Required number = 60 + (50% of 60)
$= 60 + 30 = 90$
Alternatively, finding 50% more than 60 is equivalent to finding 150% of 60 (since 100% + 50% = 150%).
Required number = 150% of 60
$= \frac{150}{100} \times 60$
$ = \frac{\cancel{150}^{3}}{\cancel{100}_{2}} \times 60 = \frac{3}{2} \times 60 $
$ = 3 \times \cancel{30}^{} = 90 $
In both methods, the number is 90.
The blank should be filled with 90.
Question 37. John sells a bat for ₹ 75 and suffers a loss of ₹ 8. The cost price of the bat is ________.
Answer:
We are given the selling price and the amount of loss.
Selling Price (SP) = ₹ 75
Loss = ₹ 8
When there is a loss, the cost price (CP) is related to the selling price and loss by the formula:
Loss = Cost Price - Selling Price
Rearranging the formula to find the Cost Price:
Cost Price = Selling Price + Loss
Substitute the given values into the formula:
Cost Price = ₹ 75 + ₹ 8
Cost Price = ₹ 83
So, the cost price of the bat is ₹ 83.
The blank should be filled with ₹ 83.
Question 38. If the price of sugar is decreased by 20%, then the new price of 3kg sugar originally costing ₹ 120 will be ________.
Answer:
We are given the original cost of 3 kg sugar and the percentage decrease in price.
Original cost of 3 kg sugar = ₹ 120
Percentage decrease in price = 20%
First, we need to find the amount of decrease in the price of 3 kg sugar.
Amount of decrease = 20% of ₹ 120.
This can be calculated as:
$20\% \text{ of } \textsf{₹} \, 120 = \frac{20}{100} \times 120$
Calculate the value:
$ \frac{20}{100} \times 120 = \frac{\cancel{20}^{1}}{\cancel{100}_{5}} \times 120 = \frac{1}{5} \times 120 $
$ \frac{1}{5} \times 120 = 24 $
So, the amount of decrease in price is ₹ 24.
To find the new price, we subtract the amount of decrease from the original cost.
New price = Original cost - Amount of decrease
$= \textsf{₹} \, 120 - \textsf{₹} \, 24 = \textsf{₹} \, 96$
Alternatively, if the price is decreased by 20%, the new price will be (100% - 20%) = 80% of the original price.
New price = 80% of ₹ 120
$= \frac{80}{100} \times 120$
$ = \frac{\cancel{80}^{4}}{\cancel{100}_{5}} \times 120 = \frac{4}{5} \times 120 $
$ = 4 \times \cancel{24}^{} = 96 $
In both methods, the new price of 3 kg sugar is ₹ 96.
The blank should be filled with ₹ 96.
Question 39. Mohini bought a cow for ₹ 9000 and sold it at a loss of ₹ 900. The selling price of the cow is ________.
Answer:
We are given the cost price of the cow and the amount of loss incurred on selling it.
Cost Price (CP) = ₹ 9000
Loss = ₹ 900
When an item is sold at a loss, the Selling Price (SP) is calculated by subtracting the loss from the Cost Price.
The formula is:
Selling Price = Cost Price - Loss
Substitute the given values into the formula:
Selling Price = $\textsf{₹}$ 9000 - $\textsf{₹}$ 900
Selling Price = $\textsf{₹}$ 8100
So, the selling price of the cow is ₹ 8100.
The blank should be filled with ₹ 8100.
Question 40. Devangi buys a chair for ₹ 700 and sells it for ₹ 750. She earns a profit of ________ % in the transaction.
Answer:
We are given the cost price and selling price of the chair. We need to find the profit percentage.
Cost Price (CP) = ₹ 700
Selling Price (SP) = ₹ 750
Since the selling price (₹ 750) is greater than the cost price (₹ 700), there is a profit.
Profit = Selling Price - Cost Price
Profit = $\textsf{₹}$ 750 - $\textsf{₹}$ 700 = $\textsf{₹}$ 50
To find the profit percentage, we use the formula:
Profit Percentage $= \frac{\text{Profit}}{\text{Cost Price}} \times 100\%$
Profit Percentage $= \frac{\textsf{₹} \, 50}{\textsf{₹} \, 700} \times 100\%$.
Calculate the value:
$ \frac{50}{700} \times 100\% = \frac{\cancel{50}^{1}}{\cancel{700}_{14}} \times 100\% = \frac{1}{14} \times 100\% $
$ = \frac{100}{14}\% $
$ = \frac{\cancel{100}^{50}}{\cancel{14}_{7}}\% = \frac{50}{7}\% $
We can express $\frac{50}{7}$ as a mixed number:
When 50 is divided by 7, the quotient is 7 and the remainder is 1.
So, $\frac{50}{7} = 7\frac{1}{7}$.
Thus, the profit percentage is $7\frac{1}{7}\%$.
Therefore, she earns a profit of $7\frac{1}{7}$ % in the transaction.
The blank should be filled with $7\frac{1}{7}$.
Question 41. Sonal bought a bed sheet for ₹ 400 and sold it for ₹ 440. Her ____% is _____.
Answer:
We are given the cost price and selling price of the bed sheet. We need to determine if it's a profit or loss and calculate the percentage.
Cost Price (CP) = ₹ 400
Selling Price (SP) = ₹ 440
Since the selling price (₹ 440) is greater than the cost price (₹ 400), there is a profit.
Profit = Selling Price - Cost Price
Profit = $\textsf{₹}$ 440 - $\textsf{₹}$ 400 = $\textsf{₹}$ 40
Now, we calculate the profit percentage using the formula:
Profit Percentage $= \frac{\text{Profit}}{\text{Cost Price}} \times 100\%$
Profit Percentage $= \frac{\textsf{₹} \, 40}{\textsf{₹} \, 400} \times 100\%$.
Calculate the value:
$ \frac{40}{400} \times 100\% = \frac{\cancel{40}^{1}}{\cancel{400}_{10}} \times 100\% = \frac{1}{10} \times 100\% $
$ = \frac{100}{10}\% = 10\% $
So, Sonal earns a profit of 10%.
The statement is "Her ____% is _____." This suggests filling in the type of gain (profit or loss) and the percentage value.
Therefore, her profit % is 10.
Question 42. Nasim bought a pen for ₹ 60 and sold it for ₹ 54. His _____% is ________.
Answer:
We are given the cost price and selling price of the pen. We need to determine if it's a profit or loss and calculate the percentage.
Cost Price (CP) = ₹ 60
Selling Price (SP) = ₹ 54
Since the selling price (₹ 54) is less than the cost price (₹ 60), there is a loss.
Loss = Cost Price - Selling Price
Loss = $\textsf{₹}$ 60 - $\textsf{₹}$ 54 = $\textsf{₹}$ 6
Now, we calculate the loss percentage using the formula:
Loss Percentage $= \frac{\text{Loss}}{\text{Cost Price}} \times 100\%$
Loss Percentage $= \frac{\textsf{₹} \, 6}{\textsf{₹} \, 60} \times 100\%$.
Calculate the value:
$ \frac{6}{60} \times 100\% = \frac{\cancel{6}^{1}}{\cancel{60}_{10}} \times 100\% = \frac{1}{10} \times 100\% $
$ = \frac{100}{10}\% = 10\% $
So, Nasim incurs a loss of 10%.
The statement is "His _____% is ________." This suggests filling in the type of gain (profit or loss) and the percentage value.
Therefore, his loss % is 10.
Question 43. Aahuti purchased a house for ₹ 50,59,700 and spent ₹ 40300 on its repairs. To make a profit of 5%, she should sell the house for ₹ ________.
Answer:
We are given the purchase price of the house and the repair costs. We also know the desired profit percentage.
The total cost price of the house includes the purchase price and the repair costs.
Purchase Price = ₹ 50,59,700
Repair Costs = ₹ 40,300
Total Cost Price (CP) = Purchase Price + Repair Costs
CP = $\textsf{₹}$ 50,59,700 + $\textsf{₹}$ 40,300
CP = $\textsf{₹}$ 51,00,000
Desired Profit Percentage = 5%
To make a profit of 5%, she needs to sell the house at a price that is 5% more than the total cost price.
Amount of desired profit = 5% of Total Cost Price
Amount of profit = 5% of ₹ 51,00,000
$= \frac{5}{100} \times 51,00,000$
Calculate the value:
$ \frac{5}{100} \times 51,00,000 = 5 \times \frac{\cancel{51,00,000}^{51000}}{\cancel{100}_{1}} = 5 \times 51000 $
$ 5 \times 51000 = 255000 $
The amount of desired profit is ₹ 2,55,000.
To find the selling price (SP), we add the desired profit to the total cost price.
Selling Price = Total Cost Price + Amount of Profit
SP = $\textsf{₹}$ 51,00,000 + $\textsf{₹}$ 2,55,000
SP = $\textsf{₹}$ 53,55,000
Alternatively, if she wants to make a profit of 5%, the selling price should be (100% + 5%) = 105% of the total cost price.
Selling Price = 105% of ₹ 51,00,000
$= \frac{105}{100} \times 51,00,000$
$ = \frac{105}{\cancel{100}_{1}} \times \cancel{51,00,000}^{51000} = 105 \times 51000 $
Multiply 105 by 51:
$105 \times 51 = 105 \times (50 + 1) = 105 \times 50 + 105 \times 1 = 5250 + 105 = 5355$
So, $105 \times 51000 = 5355000$.
In both methods, the selling price should be ₹ 53,55,000.
The blank should be filled with 53,55,000.
Question 44. If 20 lemons are bought for ₹ 10 and sold at 5 for three rupees, then ________ in the transaction is ________%.
Answer:
To determine the profit or loss percentage, we need to compare the cost price (CP) and the selling price (SP) for the same number of items.
We are given:
Cost Price of 20 lemons = ₹ 10
Selling Price of 5 lemons = ₹ 3
Let's find the selling price of 20 lemons so we can compare it with the cost price of 20 lemons.
Since 5 lemons are sold for ₹ 3, the selling price per lemon is $\textsf{₹} \, \frac{3}{5}$.
Selling Price of 20 lemons = 20 $\times$ (Selling price per lemon)
$= 20 \times \textsf{₹} \, \frac{3}{5}$
$= \cancel{20}^{4} \times \textsf{₹} \, \frac{3}{\cancel{5}^{1}} = 4 \times \textsf{₹} \, 3 = \textsf{₹} \, 12$
So, the Selling Price of 20 lemons is ₹ 12.
Now we compare the Cost Price and Selling Price of 20 lemons:
Cost Price of 20 lemons = ₹ 10
Selling Price of 20 lemons = ₹ 12
Since Selling Price (₹ 12) > Cost Price (₹ 10), there is a profit in the transaction.
Calculate the amount of profit:
Profit = Selling Price - Cost Price
Profit = $\textsf{₹}$ 12 - $\textsf{₹}$ 10 = $\textsf{₹}$ 2
Now, calculate the profit percentage based on the cost price:
Profit Percentage $= \frac{\text{Profit}}{\text{Cost Price}} \times 100\%$
Profit Percentage $= \frac{\textsf{₹} \, 2}{\textsf{₹} \, 10} \times 100\%$
Calculate the value:
$ \frac{2}{10} \times 100\% = \frac{\cancel{2}^{1}}{\cancel{10}_{5}} \times 100\% $
$ = \frac{1}{5} \times 100\% $
$ = \frac{100}{5}\% = 20\% $
So, the profit in the transaction is 20%.
The blank should be filled to say "then profit in the transaction is 20%."
Question 45. Narain bought 120 oranges at ₹ 4 each. He sold 60 % of the oranges at ₹ 5 each and the remaining at ₹ 3.50 each. His ________ is ________%.
Answer:
First, let's calculate the total cost price (CP) of the oranges.
Number of oranges bought = 120
Cost per orange = ₹ 4
Total Cost Price = Number of oranges $\times$ Cost per orange
CP = $120 \times \textsf{₹} \, 4 = \textsf{₹} \, 480$
Next, let's find the number of oranges sold at the first price (60% of the oranges).
Number of oranges in the first batch = 60% of 120
$ = \frac{60}{100} \times 120 = \frac{6}{\cancel{10}} \times 12\cancel{0}^{} = 6 \times 12 = 72$
So, 72 oranges were sold at ₹ 5 each.
Selling Price of the first batch = $72 \times \textsf{₹} \, 5 = \textsf{₹} \, 360$
Now, let's find the number of remaining oranges and their selling price.
Number of remaining oranges = Total oranges - Number of oranges in the first batch
$= 120 - 72 = 48$
These 48 oranges were sold at ₹ 3.50 each.
Selling Price of the second batch = $48 \times \textsf{₹} \, 3.50$
$48 \times 3.5 = 48 \times \frac{7}{2} = \cancel{48}^{24} \times 7 = 24 \times 7 = 168$
Selling Price of the second batch = ₹ 168
Calculate the total selling price (SP) of all oranges.
Total Selling Price = Selling Price of the first batch + Selling Price of the second batch
SP = $\textsf{₹}$ 360 + $\textsf{₹}$ 168 = $\textsf{₹}$ 528
Compare the Total Selling Price with the Total Cost Price.
Total Cost Price = ₹ 480
Total Selling Price = ₹ 528
Since SP (₹ 528) > CP (₹ 480), there is a profit.
Calculate the amount of profit.
Profit = Total Selling Price - Total Cost Price
Profit = $\textsf{₹}$ 528 - $\textsf{₹}$ 480 = $\textsf{₹}$ 48
Now, calculate the profit percentage based on the total cost price.
Profit Percentage $= \frac{\text{Profit}}{\text{Total Cost Price}} \times 100\%$
Profit Percentage $= \frac{\textsf{₹} \, 48}{\textsf{₹} \, 480} \times 100\%$.
Calculate the value:
$ \frac{48}{480} \times 100\% = \frac{\cancel{48}^{1}}{\cancel{480}_{10}} \times 100\% = \frac{1}{10} \times 100\% $
$ = \frac{100}{10}\% = 10\% $
So, Narain makes a profit of 10% in the transaction.
The statement is "His ________ is ________%." This suggests filling in the type of gain (profit or loss) and the percentage value.
Therefore, his profit is 10%.
Question 46. A fruit seller purchased 20 kg of apples at ₹ 50 per kg. Out of these, 5% of the apples were found to be rotten. If he sells the remaining apples at ₹ 60 per kg, then his _________is _________%.
Answer:
Given:
Quantity of apples purchased = 20 kg
Cost per kg = ₹ 50
Percentage of rotten apples = 5%
Selling price of remaining apples per kg = ₹ 60
To Find:
Whether the transaction results in a profit or loss and the percentage.
Solution:
First, let's find the total cost price (CP) of the apples.
Total Cost Price (CP) = Quantity purchased $\times$ Cost per kg
$CP = 20 \times \textsf{₹} \, 50$
$CP = \textsf{₹} \, 1000$
Next, find the quantity of rotten apples.
Rotten apples = 5% of total quantity
$= 5\% \text{ of } 20 \, \text{kg} = \frac{5}{100} \times 20 \, \text{kg}$
$= \frac{5}{\cancel{100}_{5}} \times \cancel{20}^{1} \, \text{kg} = \frac{5}{5} \, \text{kg} = 1 \, \text{kg}$
So, 1 kg of apples were rotten.
Find the quantity of apples that are good and can be sold.
Quantity of remaining apples = Total quantity - Rotten apples
$= 20 \, \text{kg} - 1 \, \text{kg} = 19 \, \text{kg}$
Now, find the total selling price (SP) of the remaining apples.
Selling Price (SP) = Quantity of remaining apples $\times$ Selling price per kg
$SP = 19 \times \textsf{₹} \, 60$
$SP = \textsf{₹} \, 1140$
Compare the Selling Price and Cost Price.
$SP = \textsf{₹} \, 1140$
$CP = \textsf{₹} \, 1000$
Since $SP > CP$, there is a profit.
Calculate the amount of profit.
Profit = Selling Price - Cost Price
Profit = $\textsf{₹}$ 1140 - $\textsf{₹}$ 1000 = $\textsf{₹}$ 140
Finally, calculate the profit percentage.
Profit Percentage $= \frac{\text{Profit}}{\text{Cost Price}} \times 100\%$
Profit Percentage $= \frac{\textsf{₹} \, 140}{\textsf{₹} \, 1000} \times 100\%$
$= \frac{140}{1000} \times 100\% = \frac{14\cancel{0}}{\cancel{100\cancel{0}}} \times 1\cancel{00}\% = \frac{14}{1}\% = 14\%$
So, the profit percentage is 14%.
The blank should be filled to state the type of gain and the percentage.
Therefore, his profit is 14%.
Question 47. Interest on ₹ 3000 at 10% per annum for a period of 3 years is ________.
Answer:
Given:
Principal Amount (P) = ₹ 3000
Rate of Interest (R) = 10% per annum
Time Period (T) = 3 years
To Find:
Simple Interest
Solution:
We use the formula for Simple Interest (SI):
$SI = \frac{P \times R \times T}{100}$
Substitute the given values into the formula:
$SI = \frac{\textsf{₹} \, 3000 \times 10 \times 3}{100}$
Calculate the value:
$ SI = \frac{30000 \times 3}{100} $
$ SI = \frac{90000}{100} $
$ SI = \frac{\cancel{90000}^{900}}{\cancel{100}_{1}} $
$ SI = 900 $
The Simple Interest is ₹ 900.
The blank should be filled with the amount of interest.
Therefore, Interest on ₹ 3000 at 10% per annum for a period of 3 years is ₹ 900.
Question 48. Amount obtained by depositing ₹ 20,000 at 8 % per annum for six months is ________.
Answer:
Given:
Principal Amount (P) = ₹ 20,000
Rate of Interest (R) = 8% per annum
Time Period (T) = six months
To Find:
Amount obtained (Principal + Simple Interest)
Solution:
First, convert the time period from months to years.
1 year = 12 months
Time Period (T) $= \frac{6}{12} \, \text{years} = \frac{1}{2} \, \text{years}$.
Now, calculate the Simple Interest (SI) using the formula:
$SI = \frac{P \times R \times T}{100}$
Substitute the given values into the formula:
$SI = \frac{\textsf{₹} \, 20000 \times 8 \times \frac{1}{2}}{100}$
Calculate the value:
$ SI = \frac{20000 \times 8 \times 1}{100 \times 2} $
$ SI = \frac{20000 \times 8}{200} $
$ SI = \frac{160000}{200} $
$ SI = \frac{\cancel{160000}^{1600}}{\cancel{200}_{2}} $
$ SI = \frac{1600}{2} = 800 $
The Simple Interest is ₹ 800.
The Amount obtained is the sum of the Principal and the Simple Interest.
Amount (A) = Principal (P) + Simple Interest (SI)
$A = \textsf{₹} \, 20000 + \textsf{₹} \, 800$
$A = \textsf{₹} \, 20800$
The blank should be filled with the total amount.
Therefore, Amount obtained by depositing ₹ 20,000 at 8 % per annum for six months is ₹ 20,800.
Question 49. Interest on ₹ 12500 at 18% per annum for a period of 2 years and 4 months is ________.
Answer:
Given:
Principal Amount (P) = ₹ 12500
Rate of Interest (R) = 18% per annum
Time Period (T) = 2 years and 4 months
To Find:
Simple Interest
Solution:
First, convert the time period entirely into years.
2 years and 4 months = 2 years $+ \frac{4}{12}$ years
$ = 2 + \frac{\cancel{4}^{1}}{\cancel{12}_{3}}$ years $= 2 + \frac{1}{3}$ years
$ = \frac{2 \times 3 + 1}{3}$ years $= \frac{6 + 1}{3}$ years $= \frac{7}{3}$ years.
Time Period (T) $= \frac{7}{3}$ years.
Now, calculate the Simple Interest (SI) using the formula:
$SI = \frac{P \times R \times T}{100}$
Substitute the given values into the formula:
$SI = \frac{\textsf{₹} \, 12500 \times 18 \times \frac{7}{3}}{100}$
Calculate the value:
$ SI = \frac{12500 \times 18 \times 7}{100 \times 3} $
Simplify the denominator and numerator:
$ SI = \frac{12500 \times \cancel{18}^{6} \times 7}{100 \times \cancel{3}^{1}} $
$ SI = \frac{12500 \times 6 \times 7}{100} $
$ SI = \frac{\cancel{12500}^{125} \times 6 \times 7}{\cancel{100}_{1}} $
$ SI = 125 \times 6 \times 7 $
$ SI = 125 \times 42 $
Multiply 125 by 42:
$125 \times 42 = 125 \times (40 + 2) = 125 \times 40 + 125 \times 2 = 5000 + 250 = 5250$
The Simple Interest is ₹ 5250.
The blank should be filled with the amount of interest.
Therefore, Interest on ₹ 12500 at 18% per annum for a period of 2 years and 4 months is ₹ 5250.
Question 50. 25 ml is _________ per cent of 5 litres.
Answer:
To find what percentage one quantity is of another, both quantities must be in the same units.
We are given 25 ml and 5 litres.
Convert litres to millilitres:
1 litre = 1000 ml
5 litres = $5 \times 1000 \, \text{ml} = 5000 \, \text{ml}$
Now, we want to find what percentage 25 ml is of 5000 ml.
We form the fraction: $\frac{\text{Part}}{\text{Whole}} = \frac{25 \, \text{ml}}{5000 \, \text{ml}}$.
The units (ml) cancel out, leaving the fraction $\frac{25}{5000}$.
Now, convert the fraction $\frac{25}{5000}$ to a percentage by multiplying by 100%:
Percentage $= \frac{25}{5000} \times 100\%$.
Calculate the value:
$ \frac{25}{5000} \times 100\% = \frac{25}{\cancel{5000}_{50}} \times \cancel{100}^{1}\% $
$ = \frac{25}{50}\% $
Simplify the fraction $\frac{25}{50}$:
$ \frac{\cancel{25}^{1}}{\cancel{50}_{2}}\% = \frac{1}{2}\% $
Express the fraction as a decimal:
$ \frac{1}{2}\% = 0.5\% $
So, 25 ml is 0.5% of 5 litres.
The blank should be filled with 0.5.
Question 51. If A is increased by 20%, it equals B. If B is decreased by 50%, it equals C. Then __________ % of A is equal to C.
Answer:
Given:
A increased by 20% equals B.
B decreased by 50% equals C.
To Find:
What percentage of A is equal to C.
Solution:
According to the first statement:
If A is increased by 20%, it equals B.
$B = A + 20\% \text{ of } A$
$B = A + \frac{20}{100} \times A$
$B = A + \frac{1}{5} A$
$B = \left(1 + \frac{1}{5}\right)A = \left(\frac{5+1}{5}\right)A = \frac{6}{5}A$
According to the second statement:
If B is decreased by 50%, it equals C.
$C = B - 50\% \text{ of } B$
$C = B - \frac{50}{100} \times B$
$C = B - \frac{1}{2} B$
$C = \left(1 - \frac{1}{2}\right)B = \left(\frac{2-1}{2}\right)B = \frac{1}{2}B$
Now we have $C = \frac{1}{2}B$ and we know $B = \frac{6}{5}A$. Substitute the value of B into the equation for C:
$C = \frac{1}{2} \times \left(\frac{6}{5}A\right)$
$C = \frac{1 \times 6}{2 \times 5} A$
$C = \frac{\cancel{6}^{3}}{\cancel{10}_{5}} A$
$C = \frac{3}{5}A$
We need to express $\frac{3}{5}A$ as a percentage of A. To do this, we convert the fraction $\frac{3}{5}$ into a percentage by multiplying by 100%.
Percentage $= \frac{3}{5} \times 100\%$
$= \frac{3}{\cancel{5}^{1}} \times \cancel{100}^{20}\%$
$= 3 \times 20\% = 60\%$
So, C is 60% of A.
The blank should be filled with the percentage value.
Therefore, 60 % of A is equal to C.
Question 52. Interest = $\frac{ P \;×\; R \;×\; T}{100}$ , where
T is ____________
R% is ____________ and
P is ____________.
Answer:
The formula for Simple Interest (SI) is given as $SI = \frac{ P \times R \times T}{100}$.
In this formula, the letters P, R, and T represent specific quantities related to the interest calculation.
T represents the Time Period for which the principal amount is lent or deposited. This time is usually measured in years.
R% represents the Rate of Interest per annum (per year). The rate is given as a percentage (R%). In the formula, R is used without the percentage sign, meaning R is the numerical value of the rate (e.g., if the rate is 10%, R = 10).
P represents the Principal Amount. This is the initial sum of money borrowed, lent, or deposited.
Filling the blanks:
T is Time Period
R% is Rate of Interest
P is Principal Amount
Question 53. The difference of interest for 2 years and 3 years on a sum of ₹ 2100 at 8% per annum is _________.
Answer:
Given:
Principal Amount (P) = ₹ 2100
Rate of Interest (R) = 8% per annum
Time Period 1 (T1) = 2 years
Time Period 2 (T2) = 3 years
To Find:
The difference between the simple interest for 3 years and the simple interest for 2 years.
Solution:
We will calculate the Simple Interest (SI) for each time period using the formula $SI = \frac{P \times R \times T}{100}$.
Calculate the Simple Interest for 2 years (SI1):
$SI1 = \frac{P \times R \times T1}{100}$
$SI1 = \frac{\textsf{₹} \, 2100 \times 8 \times 2}{100}$
$SI1 = \frac{\cancel{2100}^{21} \times 8 \times 2}{\cancel{100}_{1}}$
$SI1 = 21 \times 16$
$21 \times 16 = 336$
SI1 = ₹ 336
Calculate the Simple Interest for 3 years (SI2):
$SI2 = \frac{P \times R \times T2}{100}$
$SI2 = \frac{\textsf{₹} \, 2100 \times 8 \times 3}{100}$
$SI2 = \frac{\cancel{2100}^{21} \times 8 \times 3}{\cancel{100}_{1}}$
$SI2 = 21 \times 24$
$21 \times 24 = 504$
SI2 = ₹ 504
Find the difference in the interest:
Difference = SI2 - SI1
Difference = $\textsf{₹}$ 504 - $\textsf{₹}$ 336
Difference = $\textsf{₹}$ 168
Alternatively, for simple interest, the interest for each year is the same. The difference in interest for 3 years and 2 years is simply the interest for 1 year.
Time difference = 3 years - 2 years = 1 year.
Interest for 1 year $= \frac{P \times R \times 1}{100}$
$= \frac{\textsf{₹} \, 2100 \times 8 \times 1}{100}$
$= \frac{\cancel{2100}^{21} \times 8}{\cancel{100}_{1}} = 21 \times 8 = 168$
The difference in interest is ₹ 168.
The blank should be filled with the difference in interest.
Therefore, the difference of interest for 2 years and 3 years on a sum of ₹ 2100 at 8% per annum is ₹ 168.
Question 54. To convert a fraction into a per cent, we _________ it by 100.
Answer:
The question asks how to convert a fraction into a percentage.
By definition, a percentage is a fraction out of 100. To express any quantity as a fraction of 100, we multiply it by 100%.
For example, to convert the fraction $\frac{1}{2}$ to a percentage:
$\frac{1}{2} \times 100\% = 50\%$
When we multiply a fraction by 100%, we are essentially multiplying the fraction by the number 100 and including the percentage symbol (which itself means '/100').
Therefore, to convert a fraction into a per cent, we multiply it by 100 (and add the % symbol).
The blank should be filled with the word multiply.
To convert a fraction into a per cent, we multiply it by 100.
Question 55. To convert a decimal into a per cent, we shift the decimal point two places to the _________.
Answer:
The question asks how to convert a decimal into a percentage using decimal point manipulation.
Converting a decimal to a percentage involves multiplying the decimal by 100. Multiplying a number by 100 has the effect of moving the decimal point two places to the right.
For example:
Convert 0.5 to a percentage: $0.5 \times 100 = 50$. So, 0.5 = 50%.
Moving the decimal point two places to the right in 0.5 gives 50.
Convert 0.25 to a percentage: $0.25 \times 100 = 25$. So, 0.25 = 25%.
Moving the decimal point two places to the right in 0.25 gives 25.
Convert 1.2 to a percentage: $1.2 \times 100 = 120$. So, 1.2 = 120%.
Moving the decimal point two places to the right in 1.2 gives 120.
In each case, the decimal point is shifted two places to the right.
The blank should be filled with the word right.
To convert a decimal into a per cent, we shift the decimal point two places to the right.
Question 56. The _________ of interest on a sum of ₹ 2000 at the rate of 6% per annum for $1\frac{1}{2}$ years and 2 years is ₹ 420.
Answer:
Given:
Principal Amount (P) = ₹ 2000
Rate of Interest (R) = 6% per annum
Time Period 1 (T1) = $1\frac{1}{2}$ years = $\frac{3}{2}$ years
Time Period 2 (T2) = 2 years
Result = ₹ 420
To Find:
The relationship (sum or difference) between the interests for the two time periods that equals ₹ 420.
Solution:
We need to calculate the Simple Interest (SI) for each time period using the formula $SI = \frac{P \times R \times T}{100}$.
Calculate the Simple Interest for $1\frac{1}{2}$ years (SI1):
$SI1 = \frac{P \times R \times T1}{100}$
$SI1 = \frac{\textsf{₹} \, 2000 \times 6 \times \frac{3}{2}}{100}$
$SI1 = \frac{2000 \times 6 \times 3}{100 \times 2}$
$SI1 = \frac{2000 \times 18}{200}$
$SI1 = \frac{36000}{200}$
$SI1 = \frac{\cancel{36000}^{360}}{\cancel{200}_{2}}$
$SI1 = \frac{360}{2} = 180$
SI1 = ₹ 180
Calculate the Simple Interest for 2 years (SI2):
$SI2 = \frac{P \times R \times T2}{100}$
$SI2 = \frac{\textsf{₹} \, 2000 \times 6 \times 2}{100}$
$SI2 = \frac{2000 \times 12}{100}$
$SI2 = \frac{24000}{100}$
$SI2 = \frac{\cancel{24000}^{240}}{\cancel{100}_{1}}$
$SI2 = 240$
SI2 = ₹ 240
Now, let's see how SI1, SI2, and ₹ 420 are related.
Check the difference: SI2 - SI1 = ₹ 240 - ₹ 180 = ₹ 60.
Check the sum: SI1 + SI2 = ₹ 180 + ₹ 240 = ₹ 420.
The given value ₹ 420 is the sum of the interests for the two time periods.
The blank should be filled with the word that describes adding the interests.
Therefore, the blank should be filled with sum.
The sum of interest on a sum of ₹ 2000 at the rate of 6% per annum for $1\frac{1}{2}$ years and 2 years is ₹ 420.
Question 57. When converted into percentage, the value of 6.5 is _________ than 100%.
Answer:
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent symbol.
The given decimal is 6.5.
Convert 6.5 into a percentage:
$6.5 \times 100\% = 650\%$
Now, we need to compare 650% with 100%.
Since $650 > 100$, we have $650\% > 100\%$.
So, when converted into percentage, the value of 6.5 (which is 650%) is greater than 100%.
The blank should be filled with the words greater.
When converted into percentage, the value of 6.5 is greater than 100%.
In questions 58 and 59, copy each number line. Fill in the blanks so that each mark on the number line is labelled with a per cent, a fraction and a decimal. Write all fractions in lowest terms.
Question 58.

Answer:
Assuming the number line is divided into 10 equal parts between 0 and 1, the marks correspond to fractions $\frac{0}{10}, \frac{1}{10}, \frac{2}{10}, ..., \frac{10}{10}$.
We will provide the percentage, fraction (in lowest terms), and decimal for each tenth mark on the number line.
At the start (0):
Percentage: 0%
Fraction: $\frac{0}{1}$
Decimal: 0.0
At the 1st mark (1/10):
Percentage: 10%
Fraction: $\frac{1}{10}$
Decimal: 0.1
At the 2nd mark (2/10):
Percentage: 20%
Fraction: $\frac{2}{10} = \frac{1}{5}$
Decimal: 0.2
At the 3rd mark (3/10):
Percentage: 30%
Fraction: $\frac{3}{10}$
Decimal: 0.3
At the 4th mark (4/10):
Percentage: 40%
Fraction: $\frac{4}{10} = \frac{2}{5}$
Decimal: 0.4
At the 5th mark (5/10):
Percentage: 50%
Fraction: $\frac{5}{10} = \frac{1}{2}$
Decimal: 0.5
At the 6th mark (6/10):
Percentage: 60%
Fraction: $\frac{6}{10} = \frac{3}{5}$
Decimal: 0.6
At the 7th mark (7/10):
Percentage: 70%
Fraction: $\frac{7}{10}$
Decimal: 0.7
At the 8th mark (8/10):
Percentage: 80%
Fraction: $\frac{8}{10} = \frac{4}{5}$
Decimal: 0.8
At the 9th mark (9/10):
Percentage: 90%
Fraction: $\frac{9}{10}$
Decimal: 0.9
At the end (1 or 10/10):
Percentage: 100%
Fraction: $\frac{10}{10} = 1$
Decimal: 1.0
Question 59.

Answer:
The number line is divided into 4 equal parts between 0 and 1. The marks correspond to fractions $\frac{0}{4}, \frac{1}{4}, \frac{2}{4}, \frac{3}{4}, \frac{4}{4}$.
We will provide the percentage, fraction (in lowest terms), and decimal for each of these marks.
At the start (0):
Percentage: 0%
Fraction: $\frac{0}{1}$
Decimal: 0.0
At the 1st mark (1/4):
Percentage: 25%
Fraction: $\frac{1}{4}$
Decimal: 0.25
At the 2nd mark (2/4):
Percentage: 50%
Fraction: $\frac{2}{4} = \frac{1}{2}$
Decimal: 0.5
At the 3rd mark (3/4):
Percentage: 75%
Fraction: $\frac{3}{4}$
Decimal: 0.75
At the end (1 or 4/4):
Percentage: 100%
Fraction: $\frac{4}{4} = 1$
Decimal: 1.0
Question 60 to 79 (True or False)
In questions 60 to 79, state whether the statements are True or False.
Question 60. $\frac{2}{3}$ = $66\frac{2}{3}$ %
Answer:
We need to verify if the fraction $\frac{2}{3}$ is equal to $66\frac{2}{3}$ as a percentage.
First, convert the mixed number percentage $66\frac{2}{3}\%$ into a fraction.
A percentage is a fraction out of 100. So, $66\frac{2}{3}\% = \frac{66\frac{2}{3}}{100}$.
Convert the mixed number $66\frac{2}{3}$ into an improper fraction:
$66\frac{2}{3} = \frac{(66 \times 3) + 2}{3} = \frac{198 + 2}{3} = \frac{200}{3}$.
Now substitute this improper fraction back into the percentage expression:
$66\frac{2}{3}\% = \frac{\frac{200}{3}}{100}$.
To divide by 100, we multiply by the reciprocal of 100, which is $\frac{1}{100}$:
$\frac{\frac{200}{3}}{100} = \frac{200}{3} \times \frac{1}{100} = \frac{200}{300}$.
Simplify the fraction $\frac{200}{300}$ by dividing both the numerator and denominator by their greatest common divisor, which is 100:
$\frac{\cancel{200}^{2}}{\cancel{300}_{3}} = \frac{2}{3}$.
The value of $66\frac{2}{3}\%$ is indeed $\frac{2}{3}$.
Therefore, the statement $\frac{2}{3}$ = $66\frac{2}{3}$ % is True.
Question 61. When an improper fraction is converted into percentage then the answer can also be less than 100.
Answer:
An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
Let the improper fraction be represented as $\frac{a}{b}$, where $a \geq b$ and $b \neq 0$.
To convert any fraction into a percentage, we multiply the fraction by 100.
Percentage $= \text{Fraction} \times 100\%$.
For an improper fraction $\frac{a}{b}$, the percentage is $\frac{a}{b} \times 100\%$.
Since $a \geq b$ for an improper fraction, it implies that $\frac{a}{b} \geq 1$.
If a number is greater than or equal to 1, multiplying it by 100 will result in a number that is greater than or equal to 100.
So, $\frac{a}{b} \times 100\% \geq 1 \times 100\%$, which means $\frac{a}{b} \times 100\% \geq 100\%$.
Examples:
Convert the improper fraction $\frac{3}{2}$ to a percentage: $\frac{3}{2} \times 100\% = 1.5 \times 100\% = 150\%$.
Convert the improper fraction $\frac{5}{4}$ to a percentage: $\frac{5}{4} \times 100% = 1.25 \times 100\% = 125\%$.
Convert the improper fraction $\frac{7}{7}$ to a percentage: $\frac{7}{7} \times 100% = 1 \times 100\% = 100\%$.
In all cases where the fraction is improper ($a \geq b$), the resulting percentage is 100% or more. It is never less than 100%.
Thus, the statement that when an improper fraction is converted into percentage then the answer can also be less than 100 is false.
The final answer is False.
Question 62. 8 hours is 50% of 4 days.
Answer:
We need to compare 8 hours with 50% of 4 days.
First, let's convert 4 days into hours.
We know that 1 day = 24 hours.
So, 4 days = $4 \times 24$ hours.
Calculate $4 \times 24$:
$4 \times 24 = 96$ hours.
Now, we need to find 50% of 96 hours.
50% can be written as a fraction $\frac{50}{100}$ or simplified as $\frac{1}{2}$.
50% of 96 hours = $\frac{50}{100} \times 96$ hours = $\frac{1}{2} \times 96$ hours.
Calculate $\frac{1}{2} \times 96$:
$\frac{1}{2} \times 96 = \frac{96}{2} = 48$ hours.
So, 50% of 4 days is equal to 48 hours.
The statement claims that 8 hours is 50% of 4 days. This means 8 hours should be equal to 48 hours.
Comparing the two values: $8$ hours $\neq$ $48$ hours.
The statement is false.
The final answer is False.
Question 63. The interest on 350 at 5% per annum for 73 days is ₹ 35.
Answer:
Given:
Principal amount (P) = $\textsf{₹} \ 350$
Rate of interest (R) = $5\%$ per annum
Time (T) = $73$ days
To Check:
If the simple interest for the given period is $\textsf{₹} \ 35$.
Solution:
The formula for simple interest (SI) is given by:
$SI = \frac{P \times R \times T}{100}$
where P is the principal, R is the rate of interest per annum, and T is the time in years.
The given time is in days. We need to convert it into years.
There are $365$ days in a year.
$T = 73$ days = $\frac{73}{365}$ years.
Substitute the given values into the simple interest formula:
$SI = \frac{350 \times 5 \times \frac{73}{365}}{100}$
Simplify the expression:
$SI = \frac{350 \times 5 \times 73}{100 \times 365}$
We can simplify the fraction $\frac{73}{365}$ as $365 = 5 \times 73$.
So, $\frac{73}{365} = \frac{1}{5}$.
Substitute this back into the formula:
$SI = \frac{350 \times 5 \times \frac{1}{5}}{100}$
$SI = \frac{350 \times \cancel{5} \times 1}{100 \times \cancel{5}}$
$SI = \frac{350}{100}$
$SI = 3.5$
The calculated simple interest is $\textsf{₹} \ 3.50$.
The statement claims the interest is $\textsf{₹} \ 35$.
Comparing the calculated interest with the claimed interest: $\textsf{₹} \ 3.50 \neq \textsf{₹} \ 35$.
Therefore, the statement is false.
The final answer is False.
Question 64. The simple interest on a sum of ₹ P for T years at R% per annum is given by the formula: Simple Interest = $\frac{T \;×\; P \;×\; R}{100}$ .
Answer:
The formula for calculating simple interest (SI) is based on the principal amount (P), the rate of interest per annum (R), and the time period in years (T).
The standard formula for simple interest is:
$SI = \frac{P \times R \times T}{100}$
The formula given in the statement is:
$SI = \frac{T \times P \times R}{100}$
In multiplication, the order of the factors does not change the product. This property is called the commutative property of multiplication.
So, $P \times R \times T$ is equivalent to $T \times P \times R$.
Therefore, the given formula $\frac{T \times P \times R}{100}$ is mathematically the same as the standard formula $\frac{P \times R \times T}{100}$.
The statement correctly represents the formula for simple interest.
The final answer is True.
Question 65. 75% = $\frac{4}{3}$ .
Answer:
We need to verify if $75\%$ is equal to the fraction $\frac{4}{3}$.
To convert a percentage to a fraction, we divide the percentage value by 100.
$75\% = \frac{75}{100}$.
Now, we simplify the fraction $\frac{75}{100}$. Both the numerator (75) and the denominator (100) are divisible by their greatest common divisor, which is 25.
Divide the numerator by 25: $75 \div 25 = 3$.
Divide the denominator by 25: $100 \div 25 = 4$.
So, $\frac{75}{100} = \frac{3}{4}$.
Alternatively, using cancellation:
$\frac{\cancel{75}^{3}}{\cancel{100}_{4}} = \frac{3}{4}$.
Thus, $75\%$ is equal to $\frac{3}{4}$.
The statement claims that $75\% = \frac{4}{3}$.
Comparing our result with the statement: $\frac{3}{4} \neq \frac{4}{3}$.
(Note that $\frac{3}{4}$ is less than 1, while $\frac{4}{3}$ is greater than 1).
Therefore, the given statement is false.
The final answer is False.
Question 66. 12% of 120 is 100.
Answer:
We need to calculate 12% of 120 and check if the result is 100.
To find a percentage of a number, we can convert the percentage to a decimal or a fraction and then multiply by the number.
12% as a fraction is $\frac{12}{100}$.
Now, calculate 12% of 120:
$12\%$ of $120 = \frac{12}{100} \times 120$
Perform the multiplication:
$\frac{12}{100} \times 120 = \frac{12 \times 120}{100} = \frac{1440}{100}$
Divide 1440 by 100:
$\frac{1440}{100} = 14.4$
So, 12% of 120 is 14.4.
The statement claims that 12% of 120 is 100.
Comparing the calculated value with the claimed value: $14.4 \neq 100$.
Therefore, the given statement is false.
The final answer is False.
Question 67. If Ankita obtains 336 marks out of 600, then percentage of marks obtained by her is 33.6. 68. 0.018 is equivalent to 8%.
Answer:
Evaluation of Question 67:
Given:
Marks obtained by Ankita = $336$
Total marks = $600$
To Check:
If the percentage of marks obtained is $33.6\%$.
Solution:
The percentage of marks obtained is calculated as:
Percentage = $\frac{\text{Marks Obtained}}{\text{Total Marks}} \times 100\%$
Substitute the given values:
Percentage = $\frac{336}{600} \times 100\%$
Simplify the expression:
Percentage = $\frac{336}{\cancel{600}_{6}} \times \cancel{100}^{1}\%$
Percentage = $\frac{336}{6}\%$
Perform the division:
$336 \div 6 = 56$.
Percentage = $56\%$.
The percentage of marks obtained by Ankita is $56\%$.
The statement claims the percentage is $33.6\%$.
Comparing our result with the statement: $56\% \neq 33.6\%$.
Therefore, the statement for Question 67 is false.
Evaluation of Question 68:
To Check:
If $0.018$ is equivalent to $8\%$.
Solution:
To compare a decimal and a percentage, we can either convert the decimal to a percentage or the percentage to a decimal.
Method 1: Convert the decimal $0.018$ to a percentage.
To convert a decimal to a percentage, multiply by $100\%$.
$0.018 \times 100\% = 1.8\%$.
Method 2: Convert the percentage $8\%$ to a decimal.
To convert a percentage to a decimal, divide by $100$.
$8\% = \frac{8}{100} = 0.08$.
Comparing the values:
From Method 1: $1.8\% \neq 8\%$.
From Method 2: $0.018 \neq 0.08$.
Therefore, $0.018$ is not equivalent to $8\%$.
The statement for Question 68 is false.
The final answer for Question 67 is False.
The final answer for Question 68 is False.
Question 68. 0.018 is equivalent to 8%.
Answer:
To Check:
If the decimal $0.018$ is equivalent to $8\%$.
Solution:
To determine if a decimal and a percentage are equivalent, we can convert one form to the other and compare the values.
Method 1: Convert the decimal $0.018$ to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100.
$0.018 \times 100 = 1.8$.
So, $0.018$ is equivalent to $1.8\%$.
Method 2: Convert the percentage $8\%$ to a decimal.
To convert a percentage to a decimal, divide the percentage value by 100.
$8\% = \frac{8}{100} = 0.08$.
Now we compare the values:
Comparing the percentage forms: $1.8\% \neq 8\%$.
Comparing the decimal forms: $0.018 \neq 0.08$.
Since $0.018$ is equal to $1.8\%$ and not $8\%$, the statement is false.
The final answer is False.
Question 69. 50% of ₹ 50 is ₹ 25.
Answer:
We need to calculate 50% of $\textsf{₹} \ 50$ and check if the result is $\textsf{₹} \ 25$.
To find a percentage of a number, we can convert the percentage to a fraction or a decimal and then multiply by the number.
50% can be written as a fraction $\frac{50}{100}$, which simplifies to $\frac{1}{2}$.
Now, calculate 50% of $\textsf{₹} \ 50$:
$50\%$ of $\textsf{₹} \ 50 = \frac{50}{100} \times \textsf{₹} \ 50$
$50\%$ of $\textsf{₹} \ 50 = \frac{1}{2} \times \textsf{₹} \ 50$
Perform the multiplication:
$\frac{1}{2} \times \textsf{₹} \ 50 = \frac{50}{2} = \textsf{₹} \ 25$.
So, 50% of $\textsf{₹} \ 50$ is $\textsf{₹} \ 25$.
The statement claims that 50% of $\textsf{₹} \ 50$ is $\textsf{₹} \ 25$.
Comparing the calculated value with the claimed value: $\textsf{₹} \ 25 = \textsf{₹} \ 25$.
Therefore, the given statement is true.
The final answer is True.
Question 70. 250 cm is 4% of 1 km.
Answer:
We need to check if $250$ cm is equal to $4\%$ of $1$ km.
To compare quantities, they must be in the same units. Let's convert both quantities to centimeters.
Convert $1$ km to centimeters:
We know that $1$ km $= 1000$ meters.
We also know that $1$ meter $= 100$ centimeters.
So, $1$ km $= 1000 \times 100$ cm.
$1$ km $= 100000$ cm.
Now, calculate $4\%$ of $1$ km (which is $100000$ cm).
$4\%$ of $100000$ cm $= \frac{4}{100} \times 100000$ cm.
Perform the calculation:
$\frac{4}{100} \times 100000 = 4 \times \frac{100000}{100} = 4 \times 1000 = 4000$.
So, $4\%$ of $1$ km is $4000$ cm.
The statement claims that $250$ cm is $4\%$ of $1$ km. This means $250$ cm should be equal to $4000$ cm.
Comparing the two values: $250$ cm $\neq$ $4000$ cm.
Therefore, the statement is false.
The final answer is False.
Question 71. Out of 600 students of a school, 126 go for a picnic. The percentage of students that did not go for the picnic is 75.
Answer:
Given:
Total number of students = $600$
Number of students who went for the picnic = $126$
To Check:
If the percentage of students who did not go for the picnic is $75\%$.
Solution:
First, find the number of students who did not go for the picnic.
Number of students not on picnic = Total students - Number of students on picnic
Number of students not on picnic = $600 - 126$.
Perform the subtraction:
$\begin{array}{cc} & 6 & 0 & 0 \\ - & 1 & 2 & 6 \\ \hline & 4 & 7 & 4 \\ \hline \end{array}$
So, the number of students who did not go for the picnic is $474$.
Now, calculate the percentage of students who did not go for the picnic. This percentage is based on the total number of students.
Percentage not on picnic = $\frac{\text{Number of students not on picnic}}{\text{Total number of students}} \times 100\%$
Percentage not on picnic = $\frac{474}{600} \times 100\%$
Simplify the expression:
Percentage not on picnic = $\frac{474}{\cancel{600}_{6}} \times \cancel{100}^{1}\%$
Percentage not on picnic = $\frac{474}{6}\%$
Perform the division:
$474 \div 6 = 79$.
Percentage not on picnic = $79\%$.
The percentage of students who did not go for the picnic is $79\%$.
The statement claims this percentage is $75\%$.
Comparing our result with the statement: $79\% \neq 75\%$.
Therefore, the statement is false.
The final answer is False.
Question 72. By selling a book for ₹ 50, a shopkeeper suffers a loss of 10%. The cost price of the book is ₹ 60.
Answer:
Given:
Selling Price (SP) of the book = $\textsf{₹} \ 50$
Loss percentage = $10\%$
To Check:
If the Cost Price (CP) of the book is $\textsf{₹} \ 60$.
Solution:
When there is a loss, the Selling Price is calculated using the formula:
$SP = CP \times \left( \frac{100 - \text{Loss} \%}{100} \right)$
We are given SP and Loss%, and we need to find CP. Rearrange the formula to solve for CP:
$CP = SP \times \left( \frac{100}{100 - \text{Loss} \%} \right)$
Substitute the given values (SP = 50, Loss% = 10):
$CP = 50 \times \left( \frac{100}{100 - 10} \right)$
$CP = 50 \times \left( \frac{100}{90} \right)$
Simplify the fraction $\frac{100}{90}$:
$\frac{100}{90} = \frac{\cancel{100}^{10}}{\cancel{90}_{9}} = \frac{10}{9}$.
Now calculate CP:
$CP = 50 \times \frac{10}{9} = \frac{50 \times 10}{9} = \frac{500}{9}$.
Convert the improper fraction $\frac{500}{9}$ to a mixed number or decimal:
$500 \div 9 = 55$ with a remainder of $5$.
So, $\frac{500}{9} = 55\frac{5}{9}$.
As a decimal, $500 \div 9 \approx 55.56$.
The cost price is approximately $\textsf{₹} \ 55.56$.
The statement claims the cost price is $\textsf{₹} \ 60$.
Comparing our calculated CP with the claimed CP: $\textsf{₹} \ 55.56 \neq \textsf{₹} \ 60$.
Therefore, the statement is false.
The final answer is False.
Alternate Method:
Assume the cost price is $\textsf{₹} \ 60$ as given in the statement.
If the cost price is $\textsf{₹} \ 60$ and there is a loss of $10\%$, the amount of loss is $10\%$ of $\textsf{₹} \ 60$.
Loss amount = $10\%$ of $\textsf{₹} \ 60 = \frac{10}{100} \times \textsf{₹} \ 60 = \frac{1}{10} \times \textsf{₹} \ 60 = \textsf{₹} \ 6$.
The selling price is calculated as Cost Price - Loss amount.
SP = $\textsf{₹} \ 60 - \textsf{₹} \ 6 = \textsf{₹} \ 54$.
If the cost price was $\textsf{₹} \ 60$ and there was a $10\%$ loss, the selling price would be $\textsf{₹} \ 54$.
However, the given selling price is $\textsf{₹} \ 50$.
Since the calculated SP ($\textsf{₹} \ 54$) does not match the given SP ($\textsf{₹} \ 50$), the assumed cost price of $\textsf{₹} \ 60$ is incorrect.
Therefore, the statement is false.
Question 73. If a chair is bought for ₹ 2000 and is sold at a gain of 10%, then selling price of the chair is ₹ 2010.
Answer:
Given:
Cost Price (CP) of the chair = $\textsf{₹} \ 2000$
Gain percentage = $10\%$
To Check:
If the Selling Price (SP) of the chair is $\textsf{₹} \ 2010$.
Solution:
When there is a gain (profit), the Selling Price is calculated using the formula:
$SP = CP \times \left( \frac{100 + \text{Gain} \%}{100} \right)$
Substitute the given values (CP = 2000, Gain% = 10):
$SP = 2000 \times \left( \frac{100 + 10}{100} \right)$
$SP = 2000 \times \left( \frac{110}{100} \right)$
Simplify the fraction $\frac{110}{100}$:
$\frac{110}{100} = \frac{11}{10}$.
Now calculate SP:
$SP = 2000 \times \frac{11}{10}$
$SP = \frac{2000 \times 11}{10}$
$SP = \frac{22000}{10}$
$SP = 2200$.
The calculated selling price is $\textsf{₹} \ 2200$.
The statement claims the selling price is $\textsf{₹} \ 2010$.
Comparing our calculated SP with the claimed SP: $\textsf{₹} \ 2200 \neq \textsf{₹} \ 2010$.
Therefore, the statement is false.
The final answer is False.
Alternate Method:
Calculate the gain amount:
Gain amount = Gain% of CP
Gain amount = $10\%$ of $\textsf{₹} \ 2000$
Gain amount = $\frac{10}{100} \times \textsf{₹} \ 2000$
Gain amount = $\frac{1}{10} \times \textsf{₹} \ 2000 = \textsf{₹} \ 200$.
The selling price is calculated as Cost Price + Gain amount.
SP = $\textsf{₹} \ 2000 + \textsf{₹} \ 200 = \textsf{₹} \ 2200$.
The calculated selling price ($\textsf{₹} \ 2200$) does not match the claimed selling price ($\textsf{₹} \ 2010$).
Therefore, the statement is false.
Question 74. If a bicycle was bought for ₹ 650 and sold for ₹ 585, then the percentage of profit is 10.
Answer:
Given:
Cost Price (CP) of the bicycle = $\textsf{₹} \ 650$
Selling Price (SP) of the bicycle = $\textsf{₹} \ 585$
To Check:
If the percentage of profit is $10\%$.
Solution:
First, compare the Selling Price (SP) and the Cost Price (CP) to determine if there is a profit or a loss.
Since $\textsf{₹} \ 585 < \textsf{₹} \ 650$, the Selling Price is less than the Cost Price. This means there is a loss, not a profit.
Calculate the amount of loss:
Loss = CP - SP
Loss = $\textsf{₹} \ 650 - \textsf{₹} \ 585$
Perform the subtraction:
$\begin{array}{cc} & 6 & 5 & 0 \\ - & 5 & 8 & 5 \\ \hline & & 6 & 5 \\ \hline \end{array}$
The amount of loss is $\textsf{₹} \ 65$.
Now, calculate the percentage of loss. The percentage of loss is calculated on the Cost Price.
Loss Percentage = $\frac{\text{Loss}}{CP} \times 100\%$
Loss Percentage = $\frac{\textsf{₹} \ 65}{\textsf{₹} \ 650} \times 100\%$
Simplify the fraction:
$\frac{65}{650} = \frac{\cancel{65}^{1}}{\cancel{650}_{10}} = \frac{1}{10}$.
Calculate the percentage:
Loss Percentage = $\frac{1}{10} \times 100\% = 10\%$.
So, there is a loss of $10\%$.
The statement claims that the percentage of profit is $10\%$. However, our calculation shows a loss of $10\%$. A loss is the opposite of a profit.
Therefore, the statement is false.
The final answer is False.
Question 75. Sushma sold her watch for ₹ 3320 at a gain of ₹ 320. For earning a gain of 10% she should have sold the watch for ₹ 3300.
Answer:
The statement consists of two parts. We first determine the cost price based on the first part and then check if the second part is consistent with this cost price.
Given (from the first part of the statement):
Selling Price (SP) of the watch = $\textsf{₹} \ 3320$
Gain amount = $\textsf{₹} \ 320$
To Check (based on the second part of the statement):
If, for a gain of $10\%$, the selling price should be $\textsf{₹} \ 3300$.
Solution:
From the first part, we can find the Cost Price (CP) of the watch.
We know that Selling Price = Cost Price + Gain.
Rearranging the formula, Cost Price = Selling Price - Gain.
$CP = SP - \text{Gain}$
$CP = \textsf{₹} \ 3320 - \textsf{₹} \ 320$
Calculate the Cost Price:
$CP = \textsf{₹} \ 3000$.
The cost price of the watch is $\textsf{₹} \ 3000$.
Now, we use this cost price to check the second part of the statement. The second part asks if the selling price should be $\textsf{₹} \ 3300$ for a gain of $10\%$.
We need to calculate the selling price when the cost price is $\textsf{₹} \ 3000$ and the desired gain percentage is $10\%$.
Desired Gain Percentage = $10\%$.
The formula for Selling Price with a gain percentage is:
$SP' = CP \times \left( \frac{100 + \text{Gain} \%}{100} \right)$
Substitute the values $CP = \textsf{₹} \ 3000$ and Gain% = $10$ into the formula:
$SP' = 3000 \times \left( \frac{100 + 10}{100} \right)$
$SP' = 3000 \times \left( \frac{110}{100} \right)$
Simplify the expression:
$SP' = 3000 \times \frac{110}{100}$
$SP' = \frac{3000 \times 110}{100}$
$SP' = \frac{330000}{100}$
$SP' = 3300$.
The selling price required to earn a $10\%$ gain on a cost price of $\textsf{₹} \ 3000$ is $\textsf{₹} \ 3300$.
The statement claims that for earning a gain of $10\%$ she should have sold the watch for $\textsf{₹} \ 3300$.
Our calculated required selling price ($\textsf{₹} \ 3300$) matches the claimed selling price ($\textsf{₹} \ 3300$).
Therefore, the statement is true.
The final answer is True.
Question 76. Interest on ₹ 1200 for $1\frac{1}{2}$ years at the rate of 15% per annum is ₹ 180.
Answer:
Given:
Principal amount (P) = $\textsf{₹} \ 1200$
Time (T) = $1\frac{1}{2}$ years
Rate of interest (R) = $15\%$ per annum
To Check:
If the simple interest for the given period is $\textsf{₹} \ 180$.
Solution:
First, convert the mixed number time into an improper fraction:
$T = 1\frac{1}{2}$ years $= \frac{(1 \times 2) + 1}{2}$ years $= \frac{3}{2}$ years.
The formula for simple interest (SI) is given by:
$SI = \frac{P \times R \times T}{100}$
Substitute the given values into the simple interest formula:
$SI = \frac{1200 \times 15 \times \frac{3}{2}}{100}$
Simplify the expression:
$SI = \frac{1200 \times 15 \times 3}{100 \times 2}$
$SI = \frac{\cancel{1200}^{12} \times 15 \times 3}{\cancel{100} \times 2}$
$SI = \frac{12 \times 15 \times 3}{2}$
$SI = \cancel{12}^{6} \times 15 \times \frac{3}{\cancel{2}^{1}}$
$SI = 6 \times 15 \times 3$
Calculate the product:
$SI = 90 \times 3 = 270$.
The calculated simple interest is $\textsf{₹} \ 270$.
The statement claims the interest is $\textsf{₹} \ 180$.
Comparing the calculated interest with the claimed interest: $\textsf{₹} \ 270 \neq \textsf{₹} \ 180$.
Therefore, the statement is false.
The final answer is False.
Question 77. Amount received after depositing ₹ 800 for a period of 3 years at the rate of 12% per annum is ₹ 896.
Answer:
Given:
Principal amount (P) = $\textsf{₹} \ 800$
Time (T) = $3$ years
Rate of interest (R) = $12\%$ per annum
To Check:
If the amount received after the period is $\textsf{₹} \ 896$.
Solution:
The amount received is the sum of the principal and the simple interest earned over the period.
Amount = Principal + Simple Interest
First, calculate the simple interest (SI).
The formula for simple interest (SI) is:
$SI = \frac{P \times R \times T}{100}$
Substitute the given values (P = 800, R = 12, T = 3) into the formula:
$SI = \frac{800 \times 12 \times 3}{100}$
Simplify the expression:
$SI = \frac{\cancel{800}^{8} \times 12 \times 3}{\cancel{100}}$
$SI = 8 \times 12 \times 3$
Calculate the product:
$SI = 96 \times 3$
$96 \times 3 = 288$.
The simple interest is $\textsf{₹} \ 288$.
Now, calculate the total amount received:
Amount = Principal + Simple Interest
Amount = $\textsf{₹} \ 800 + \textsf{₹} \ 288$
Perform the addition:
$\begin{array}{cc} & 8 & 0 & 0 \\ + & 2 & 8 & 8 \\ \hline & 1 & 0 & 8 & 8 \\ \hline \end{array}$
The amount received is $\textsf{₹} \ 1088$.
The statement claims the amount received is $\textsf{₹} \ 896$.
Comparing the calculated amount with the claimed amount: $\textsf{₹} \ 1088 \neq \textsf{₹} \ 896$.
Therefore, the statement is false.
The final answer is False.
Question 78. ₹ 6400 were lent to Feroz and Rashmi at 15% per annum for $3\frac{1}{2}$ and 5 years respectively. The difference in the interest paid by them is ₹ 150.
Answer:
Given:
Principal amount (P) lent to both Feroz and Rashmi = $\textsf{₹} \ 6400$
Rate of interest (R) for both = $15\%$ per annum
Time for Feroz (T$_F$) = $3\frac{1}{2}$ years
Time for Rashmi (T$_R$) = $5$ years
To Check:
If the difference in the interest paid by them is $\textsf{₹} \ 150$.
Solution:
First, calculate the simple interest paid by Feroz (SI$_F$).
Convert Feroz's time into an improper fraction: $T_F = 3\frac{1}{2}$ years $= \frac{(3 \times 2) + 1}{2}$ years $= \frac{7}{2}$ years.
The formula for simple interest is $SI = \frac{P \times R \times T}{100}$.
$SI_F = \frac{P \times R \times T_F}{100}$
$SI_F = \frac{6400 \times 15 \times \frac{7}{2}}{100}$
$SI_F = \frac{6400 \times 15 \times 7}{100 \times 2}$
$SI_F = \frac{\cancel{6400}^{64} \times 15 \times 7}{\cancel{100} \times 2}$
$SI_F = \frac{\cancel{64}^{32} \times 15 \times 7}{\cancel{2}}$
$SI_F = 32 \times 15 \times 7$
Calculate the product:
$32 \times 15 = 480$
$480 \times 7 = 3360$.
$SI_F = \textsf{₹} \ 3360$.
Next, calculate the simple interest paid by Rashmi (SI$_R$).
Rashmi's time is $T_R = 5$ years.
$SI_R = \frac{P \times R \times T_R}{100}$
$SI_R = \frac{6400 \times 15 \times 5}{100}$
Simplify the expression:
$SI_R = \frac{\cancel{6400}^{64} \times 15 \times 5}{\cancel{100}}$
$SI_R = 64 \times 15 \times 5$
$SI_R = 64 \times 75$
Calculate the product $64 \times 75$:
$\begin{array}{cc}& & 6 & 4 \\ \times & & 7 & 5 \\ \hline && 3 & 2 & 0 \\ & 4 & 4 & 8 & \times \\ \hline 4 & 8 & 0 & 0 \\ \hline \end{array}$
$SI_R = \textsf{₹} \ 4800$.
Now, find the difference in the interest paid by them.
Difference in Interest = $|SI_R - SI_F|$
Difference in Interest = $|\textsf{₹} \ 4800 - \textsf{₹} \ 3360|$
Perform the subtraction:
$\begin{array}{cc} & 4 & 8 & 0 & 0 \\ - & 3 & 3 & 6 & 0 \\ \hline & 1 & 4 & 4 & 0 \\ \hline \end{array}$
The difference in interest is $\textsf{₹} \ 1440$.
The statement claims the difference in interest is $\textsf{₹} \ 150$.
Comparing our calculated difference with the claimed difference: $\textsf{₹} \ 1440 \neq \textsf{₹} \ 150$.
Therefore, the statement is false.
The final answer is False.
Question 79. A vendor purchased 720 lemons at ₹ 120 per hundred.10% of the lemons were found rotten which he sold at ₹ 50 per hundred. If he sells the remaining lemons at ₹ 125 per hundred, then his profit will be 16%.
Answer:
Given:
Total number of lemons purchased = $720$
Cost price rate = $\textsf{₹} \ 120$ per hundred
Percentage of rotten lemons = $10\%$
Selling price rate for rotten lemons = $\textsf{₹} \ 50$ per hundred
Selling price rate for remaining lemons = $\textsf{₹} \ 125$ per hundred
To Check:
If the overall profit percentage is $16\%$.
Solution:
First, calculate the total cost price (CP) of the lemons.
Number of hundreds of lemons purchased = $\frac{720}{100} = 7.2$ hundreds.
$CP = \text{Number of hundreds} \times \text{Cost per hundred}$
$CP = 7.2 \times \textsf{₹} \ 120$
$CP = \textsf{₹} \ 864$.
Next, calculate the number of rotten lemons and remaining lemons.
Number of rotten lemons = $10\%$ of $720$
Number of rotten lemons = $\frac{10}{100} \times 720 = 0.1 \times 720 = 72$ lemons.
Number of hundreds of rotten lemons = $\frac{72}{100} = 0.72$ hundreds.
Number of remaining lemons = Total lemons - Rotten lemons
Number of remaining lemons = $720 - 72 = 648$ lemons.
Number of hundreds of remaining lemons = $\frac{648}{100} = 6.48$ hundreds.
Now, calculate the selling price (SP) of the rotten lemons.
$SP_{rotten} = \text{Number of rotten hundreds} \times \text{Selling price per hundred (rotten)}$
$SP_{rotten} = 0.72 \times \textsf{₹} \ 50$
$SP_{rotten} = \textsf{₹} \ 36$.
Calculate the selling price (SP) of the remaining lemons.
$SP_{remaining} = \text{Number of remaining hundreds} \times \text{Selling price per hundred (remaining)}$
$SP_{remaining} = 6.48 \times \textsf{₹} \ 125$
$SP_{remaining} = \textsf{₹} \ 810$ (since $6.48 \times 125 = 648 \times \frac{125}{100} = 648 \times \frac{5}{4} = 162 \times 5 = 810$).
Calculate the total selling price (Total SP).
Total $SP = SP_{rotten} + SP_{remaining}$
Total $SP = \textsf{₹} \ 36 + \textsf{₹} \ 810 = \textsf{₹} \ 846$.
Compare the Total SP with the Total CP to find profit or loss.
Total CP = $\textsf{₹} \ 864$, Total SP = $\textsf{₹} \ 846$.
Since Total SP < Total CP, there is a loss.
Loss = Total CP - Total SP
Loss = $\textsf{₹} \ 864 - \textsf{₹} \ 846 = \textsf{₹} \ 18$.
Calculate the loss percentage.
Loss Percentage = $\frac{\text{Loss}}{CP} \times 100\%$
Loss Percentage = $\frac{\textsf{₹} \ 18}{\textsf{₹} \ 864} \times 100\%$
Loss Percentage = $\frac{18}{864} \times 100\%$
Simplify the fraction $\frac{18}{864}$:
$\frac{\cancel{18}^{1}}{\cancel{864}_{48}} = \frac{1}{48}$.
Loss Percentage = $\frac{1}{48} \times 100\% = \frac{100}{48}\%$.
Simplify $\frac{100}{48}$: $\frac{\cancel{100}^{25}}{\cancel{48}_{12}} = \frac{25}{12}$.
Loss Percentage = $\frac{25}{12}\%$.
The actual result is a loss of $\frac{25}{12}\%$.
The statement claims the profit is $16\%$.
Comparing our result with the statement: a loss of $\frac{25}{12}\%$ is not equal to a profit of $16\%$.
Therefore, the statement is false.
The final answer is False.
Question 80 to 140
Question 80. Find the value of x if
(i) 8% of ₹ x is ₹ 100
(ii) 32% of x kg is 400 kg
(iii) 35% of ₹ x is ₹ 280
(iv) 45% of marks x is 405.
Answer:
(i) Find x if 8% of $\textsf{₹} \text{ x is } \textsf{₹} \text{ 100}$.
We can write this as an equation:
$8\% \times x = 100$
Converting the percentage to a fraction:
$\frac{8}{100} \times x = 100$
To solve for x, multiply both sides by $\frac{100}{8}$:
$x = 100 \times \frac{100}{8}$
$x = \frac{10000}{8}$
$x = 1250$
Thus, the value of x is $\textsf{₹} \text{ 1250}$.
(ii) Find x if 32% of x kg is 400 kg.
We can write this as an equation:
$32\% \times x = 400$
Converting the percentage to a fraction:
$\frac{32}{100} \times x = 400$
To solve for x, multiply both sides by $\frac{100}{32}$:
$x = 400 \times \frac{100}{32}$
$x = \frac{40000}{32}$
$x = 1250$
Thus, the value of x is 1250 kg.
(iii) Find x if 35% of $\textsf{₹} \text{ x is } \textsf{₹} \text{ 280}$.
We can write this as an equation:
$35\% \times x = 280$
Converting the percentage to a fraction:
$\frac{35}{100} \times x = 280$
To solve for x, multiply both sides by $\frac{100}{35}$:
$x = 280 \times \frac{100}{35}$
$x = \frac{28000}{35}$
$x = 800$
Thus, the value of x is $\textsf{₹} \text{ 800}$.
(iv) Find x if 45% of marks x is 405.
We can write this as an equation:
$45\% \times x = 405$
Converting the percentage to a fraction:
$\frac{45}{100} \times x = 405$
To solve for x, multiply both sides by $\frac{100}{45}$:
$x = 405 \times \frac{100}{45}$
$x = \frac{40500}{45}$
$x = 900$
Thus, the value of x is 900 marks.
Question 81. Imagine that a 10 × 10 grid has value 300 and that this value is divided evenly among the small squares. In other words, each small square is worth 3. Use a new grid for each part of this problem, and label each grid “Value : 300.”

(a) Shade 25% of the grid. What is 25% of 300? Compare the two answers.
(b) What is the value of 25 squares?
(c) Shade 17% of the grid. What is 17% of 300? Compare the two answers.
(d) What is the value of of $\frac{1}{10}$ the grid?
Answer:
The grid is a 10 $\times$ 10 grid, which means it has $10 \times 10 = 100$ small squares.
The total value of the grid is 300, and this value is divided evenly among the 100 squares.
The value of each small square is $\frac{\text{Total Value}}{\text{Number of squares}} = \frac{300}{100} = 3$.
(a) Shade 25% of the grid. What is 25% of 300? Compare the two answers.
The grid has 100 squares. To shade 25% of the grid, we need to shade $25\%$ of 100 squares.
Number of squares to shade $= 25\% \text{ of } 100 = \frac{25}{100} \times 100 = 25$ squares.
The value of these 25 shaded squares is $25 \times (\text{value of one square}) = 25 \times 3 = 75$.
Now, we calculate 25% of the total value, which is 300.
$25\% \text{ of } 300 = \frac{25}{100} \times 300 = 0.25 \times 300 = 75$.
Comparing the two answers, the value of 25 shaded squares (75) is equal to 25% of the total grid value (75).
(b) What is the value of 25 squares?
We know that each small square is worth 3.
The value of 25 squares $= 25 \times (\text{value of one square}) = 25 \times 3 = 75$.
The value of 25 squares is 75.
(c) Shade 17% of the grid. What is 17% of 300? Compare the two answers.
The grid has 100 squares. To shade 17% of the grid, we need to shade $17\%$ of 100 squares.
Number of squares to shade $= 17\% \text{ of } 100 = \frac{17}{100} \times 100 = 17$ squares.
The value of these 17 shaded squares is $17 \times (\text{value of one square}) = 17 \times 3 = 51$.
Now, we calculate 17% of the total value, which is 300.
$17\% \text{ of } 300 = \frac{17}{100} \times 300 = 0.17 \times 300 = 51$.
Comparing the two answers, the value of 17 shaded squares (51) is equal to 17% of the total grid value (51).
(d) What is the value of of $\frac{1}{10}$ the grid?
The question asks for the value of $\frac{1}{10}$ of the total grid value.
Total grid value is 300.
Value of $\frac{1}{10}$ the grid $= \frac{1}{10} \times (\text{Total grid value}) = \frac{1}{10} \times 300$.
Value $= \frac{300}{10} = 30$.
Alternatively, $\frac{1}{10}$ of the grid means $\frac{1}{10}$ of the total number of squares.
Number of squares in $\frac{1}{10}$ of the grid $= \frac{1}{10} \times 100 = 10$ squares.
The value of these 10 squares $= 10 \times (\text{value of one square}) = 10 \times 3 = 30$.
The value of $\frac{1}{10}$ the grid is 30.
Question 82. Express $\frac{1}{6}$ as a per cent.
Answer:
To express a fraction as a percentage, we multiply the fraction by 100%.
Percentage $= \frac{1}{6} \times 100\%$
Percentage $= \frac{100}{6}\%$
Simplify the fraction:
Percentage $= \frac{\cancel{100}^{50}}{\cancel{6}_{3}}\%$
Percentage $= \frac{50}{3}\%$
We can also express this as a mixed number or a decimal:
As a mixed number:
Percentage $= 16 \frac{2}{3}\%$
As a decimal (approximately):
Percentage $\approx 16.67\%$
Question 83. Express $\frac{9}{40}$ as a per cent.
Answer:
To express a fraction as a percentage, we multiply the fraction by 100%.
Percentage $= \frac{9}{40} \times 100\%$
Percentage $= \frac{9 \times 100}{40}\%$
Percentage $= \frac{900}{40}\%$
Simplify the fraction by cancelling the common factors:
Percentage $= \frac{\cancel{900}^{90}}{\cancel{40}_{4}}\%$
Percentage $= \frac{90}{4}\%$
Percentage $= \frac{\cancel{90}^{45}}{\cancel{4}_{2}}\%$
Percentage $= \frac{45}{2}\%$
Converting the fraction to a decimal:
Percentage $= 22.5\%$
Thus, $\frac{9}{40}$ expressed as a per cent is 22.5%.
Question 84. Express $\frac{1}{100}$ as a per cent.
Answer:
To express a fraction as a percentage, we multiply the fraction by 100%.
Percentage $= \frac{1}{100} \times 100\%$
Percentage $= \frac{100}{100}\%$
Percentage $= 1\%$
Thus, $\frac{1}{100}$ expressed as a per cent is 1%.
Question 85. Express 80% as fraction in its lowest term.
Answer:
To express a percentage as a fraction, we write the percentage value over 100.
$80\% = \frac{80}{100}$
Now, we need to simplify this fraction to its lowest term by dividing the numerator and the denominator by their greatest common divisor (GCD).
The GCD of 80 and 100 is 20.
$\frac{80}{100} = \frac{80 \div 20}{100 \div 20} = \frac{4}{5}$
Alternatively, we can simplify step-by-step:
$\frac{80}{100} = \frac{\cancel{80}^{8}}{\cancel{100}_{10}}$ (Dividing by 10)
$\frac{8}{10} = \frac{\cancel{8}^{4}}{\cancel{10}_{5}}$ (Dividing by 2)
The fraction in its lowest term is $\frac{4}{5}$.
Thus, 80% expressed as a fraction in its lowest term is $\frac{4}{5}$.
Question 86. Express $33\frac{1}{3}$ % as a ratio in the lowest term.
Answer:
First, convert the mixed percentage to an improper fraction.
$33\frac{1}{3}\% = \frac{(33 \times 3) + 1}{3}\% = \frac{99 + 1}{3}\% = \frac{100}{3}\% $
Now, convert the percentage to a fraction by dividing by 100.
$\frac{100}{3}\% = \frac{\frac{100}{3}}{100}$
Simplify the complex fraction:
$\frac{\frac{100}{3}}{100} = \frac{100}{3} \times \frac{1}{100}$
Multiply the fractions:
$\frac{100}{3} \times \frac{1}{100} = \frac{100 \times 1}{3 \times 100} = \frac{100}{300}$
Simplify the fraction to its lowest term by dividing the numerator and denominator by their GCD, which is 100.
$\frac{100}{300} = \frac{100 \div 100}{300 \div 100} = \frac{1}{3}$
Alternatively, using cancellation:
$\frac{\cancel{100}^{1}}{\cancel{300}_{3}} = \frac{1}{3}$
To express the fraction $\frac{1}{3}$ as a ratio, we write it as $1:3$.
Thus, $33\frac{1}{3}\%$ expressed as a ratio in the lowest term is $1:3$.
Question 87. Express $16\frac{2}{3}$ % as a ratio in the lowest form.
Answer:
First, convert the mixed percentage to an improper fraction.
$16\frac{2}{3}\% = \frac{(16 \times 3) + 2}{3}\% = \frac{48 + 2}{3}\% = \frac{50}{3}\% $
Now, convert the percentage to a fraction by dividing by 100.
$\frac{50}{3}\% = \frac{\frac{50}{3}}{100}$
Simplify the complex fraction:
$\frac{\frac{50}{3}}{100} = \frac{50}{3} \times \frac{1}{100}$
Multiply the fractions:
$\frac{50}{3} \times \frac{1}{100} = \frac{50 \times 1}{3 \times 100} = \frac{50}{300}$
Simplify the fraction to its lowest term by dividing the numerator and denominator by their GCD, which is 50.
$\frac{50}{300} = \frac{50 \div 50}{300 \div 50} = \frac{1}{6}$
Alternatively, using cancellation:
$\frac{\cancel{50}^{1}}{\cancel{300}_{6}} = \frac{1}{6}$
To express the fraction $\frac{1}{6}$ as a ratio, we write it as $1:6$.
Thus, $16\frac{2}{3}\%$ expressed as a ratio in the lowest form is $1:6$.
Question 88. Express 150% as a ratio in the lowest form.
Answer:
To express a percentage as a fraction, we write the percentage value over 100.
$150\% = \frac{150}{100}$
Now, we need to simplify this fraction to its lowest term by dividing the numerator and the denominator by their greatest common divisor (GCD).
The GCD of 150 and 100 is 50.
$\frac{150}{100} = \frac{150 \div 50}{100 \div 50} = \frac{3}{2}$
Alternatively, we can simplify step-by-step:
$\frac{150}{100} = \frac{\cancel{150}^{15}}{\cancel{100}_{10}}$ (Dividing by 10)
$\frac{15}{10} = \frac{\cancel{15}^{3}}{\cancel{10}_{2}}$ (Dividing by 5)
The fraction in its lowest term is $\frac{3}{2}$.
To express the fraction $\frac{3}{2}$ as a ratio, we write it as $3:2$.
Thus, 150% expressed as a ratio in the lowest form is $3:2$.
Question 89. Sachin and Sanjana are calculating 23% of 800.

Now calculate 52% of 700 using both the ways described above. Which way do you find easier?
Answer:
We need to calculate 52% of 700 using two different methods.
Method 1: Converting Percentage to Fraction
To calculate 52% of 700, we can express 52% as a fraction and then multiply it by 700.
$52\% = \frac{52}{100}$
So, 52% of 700 $= \frac{52}{100} \times 700$
We can simplify this expression:
$\frac{52}{\cancel{100}_{1}} \times \cancel{700}^{7}$
Result $= 52 \times 7$
Let's perform the multiplication:
$\begin{array}{cc}& & 5 & 2 \\ \times & & & 7 \\ \hline & 3 & 6 & 4 \\ \hline \end{array}$
$52 \times 7 = 364$
So, 52% of 700 is 364.
Method 2: Converting Percentage to Decimal
To calculate 52% of 700, we can express 52% as a decimal and then multiply it by 700.
$52\% = \frac{52}{100} = 0.52$
So, 52% of 700 $= 0.52 \times 700$
We can perform the multiplication:
$0.52 \times 700 = 52 \times 7$ (since $0.52 \times 700 = (0.52 \times 100) \times 7 = 52 \times 7$)
As calculated in Method 1, $52 \times 7 = 364$.
$\begin{array}{cc}& & 0 & . & 5 & 2 \\ \times & & & & 7 & 0 & 0 \\ \hline &&& 0 & 0 & 0 & 0 \\ && 3 & 6 & 4 & 0 & \times \\ \hline && 3 & 6 & 4 & 0 & 0 \\ \hline \end{array}$
Moving the decimal point two places to the left (because 0.52 has two decimal places):
Result $= 364.00 = 364$
So, 52% of 700 is 364.
Comparison of Methods
Both methods yield the same correct answer, 364.
The ease of the method depends on the numbers involved and personal preference.
In this specific case (52% of 700), converting to a fraction ($\frac{52}{100}$) allows for easy cancellation with 700, leading to a simple multiplication ($52 \times 7$).
Converting to a decimal (0.52) also leads to $0.52 \times 700$, which simplifies to $52 \times 7$. For numbers like 700 (multiples of 100), both methods are quite efficient.
Generally, converting to a fraction might be easier when the number you are taking the percentage of is a multiple of 100 or when the percentage fraction can be significantly simplified (e.g., 25% = 1/4, 50% = 1/2).
Converting to a decimal is often straightforward for any percentage and number combination, especially when using a calculator.
For this particular problem, both methods are relatively easy. However, the fraction method with cancellation ($\frac{52}{100} \times 700 = 52 \times 7$) might feel slightly more direct due to the cancellation of the 100 in the denominator with the 700.
Therefore, I find the fraction method slightly easier for this problem because of the quick cancellation.
Question 90. Write 0.089 as a per cent.
Answer:
To express a decimal as a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
Percentage $= 0.089 \times 100\%$
Multiplying 0.089 by 100 moves the decimal point two places to the right.
$0.089 \times 100 = 8.9$
So, the percentage is $8.9\%$.
Thus, 0.089 as a per cent is 8.9%.
Question 91. Write 1.56 as a per cent.
Answer:
To express a decimal as a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
Percentage $= 1.56 \times 100\%$
Multiplying 1.56 by 100 moves the decimal point two places to the right.
$1.56 \times 100 = 156$
So, the percentage is $156\%$.
Thus, 1.56 as a per cent is 156%.
Question 92. What is 15% of 20?
Answer:
To find 15% of 20, we can express 15% as a fraction or a decimal and then multiply by 20.
Method 1: Convert Percentage to Fraction
$15\% = \frac{15}{100}$
So, 15% of 20 is:
$\frac{15}{100} \times 20$
Simplify the expression:
$\frac{15}{\cancel{100}_{5}} \times \cancel{20}^{1}$
$= \frac{15}{5} \times 1$
$= 3 \times 1$
$= 3$
Method 2: Convert Percentage to Decimal
$15\% = \frac{15}{100} = 0.15$
So, 15% of 20 is:
$0.15 \times 20$
$0.15 \times 20 = 3.00 = 3$
Using either method, the result is 3.
Thus, 15% of 20 is 3.
Question 93. What is 800% of 800?
Answer:
To find 800% of 800, we can express 800% as a fraction or a decimal and then multiply by 800.
Convert the percentage to a fraction:
$800\% = \frac{800}{100}$
Now, multiply this fraction by 800:
$800\% \text{ of } 800 = \frac{800}{100} \times 800$
We can simplify the expression by cancelling:
$= \frac{800}{\cancel{100}_{1}} \times \cancel{800}^{8}$
$= 8 \times 800$
Calculate the product:
$8 \times 800 = 6400$
Alternatively, converting to a decimal:
$800\% = \frac{800}{100} = 8$
So, 800% of 800 $= 8 \times 800 = 6400$.
Thus, 800% of 800 is 6400.
Question 94. What is 100% of 500?
Answer:
To find 100% of 500, we can express 100% as a fraction or a decimal and then multiply by 500.
Method 1: Convert Percentage to Fraction
$100\% = \frac{100}{100} = 1$
So, 100% of 500 is:
$\frac{100}{100} \times 500$
$= 1 \times 500$
$= 500$
Method 2: Convert Percentage to Decimal
$100\% = \frac{100}{100} = 1.00$
So, 100% of 500 is:
$1.00 \times 500$
$= 500$
Using either method, the result is 500.
100% of a number is the number itself.
Thus, 100% of 500 is 500.
Question 95. What per cent of 1 hour is 30 minutes?
Answer:
To find what per cent 30 minutes is of 1 hour, we first need to express both quantities in the same unit. Let's convert 1 hour into minutes.
1 hour = 60 minutes.
Now we want to find what percentage 30 minutes is of 60 minutes.
The required percentage is given by the formula:
Percentage $= \left(\frac{\text{Part}}{\text{Whole}}\right) \times 100\%$
Here, the part is 30 minutes and the whole is 60 minutes.
Percentage $= \left(\frac{30 \text{ minutes}}{60 \text{ minutes}}\right) \times 100\%$
Percentage $= \frac{30}{60} \times 100\%$
Simplify the fraction $\frac{30}{60}$:
$\frac{30}{60} = \frac{1}{2}$
Now calculate the percentage:
Percentage $= \frac{1}{2} \times 100\%$
Percentage $= \frac{100}{2}\%$
Percentage $= 50\%$
Thus, 30 minutes is 50% of 1 hour.
Question 96. What per cent of 1 day is 1 minute?
Answer:
To find what per cent 1 minute is of 1 day, we first need to express both quantities in the same unit. Let's convert 1 day into minutes.
1 day has 24 hours.
Each hour has 60 minutes.
So, 1 day $= 24 \text{ hours} \times 60 \text{ minutes/hour}$
1 day $= 1440 \text{ minutes}$.
Now we want to find what percentage 1 minute is of 1440 minutes.
The required percentage is given by the formula:
Percentage $= \left(\frac{\text{Part}}{\text{Whole}}\right) \times 100\%$
Here, the part is 1 minute and the whole is 1440 minutes.
Percentage $= \left(\frac{1 \text{ minute}}{1440 \text{ minutes}}\right) \times 100\%$
Percentage $= \frac{1}{1440} \times 100\%$
Percentage $= \frac{100}{1440}\%$
Simplify the fraction $\frac{100}{1440}$:
Divide both numerator and denominator by 10:
$\frac{\cancel{100}^{10}}{\cancel{1440}_{144}}$
Now divide both numerator and denominator by 2:
$\frac{\cancel{10}^{5}}{\cancel{144}_{72}}$
The simplified fraction is $\frac{5}{72}$.
So, the percentage is $\frac{5}{72}\%$.
We can also express this as a decimal by dividing 5 by 72:
$5 \div 72 \approx 0.06944...$
Percentage $\approx 0.0694\%$.
Thus, 1 minute is $\frac{5}{72}\%$ (or approximately 0.0694%) of 1 day.
Question 97. What per cent of 1 km is 1000 metres?
Answer:
To find what per cent 1000 metres is of 1 km, we first need to express both quantities in the same unit. Let's convert 1 km into metres.
We know that 1 kilometre = 1000 metres.
So, we want to find what percentage 1000 metres is of 1000 metres.
The required percentage is given by the formula:
Percentage $= \left(\frac{\text{Part}}{\text{Whole}}\right) \times 100\%$
Here, the part is 1000 metres and the whole is 1 km, which is equal to 1000 metres.
Percentage $= \left(\frac{1000 \text{ metres}}{1000 \text{ metres}}\right) \times 100\%$
Percentage $= \frac{1000}{1000} \times 100\%$
Simplify the fraction $\frac{1000}{1000}$:
$\frac{1000}{1000} = 1$
Now calculate the percentage:
Percentage $= 1 \times 100\%$
Percentage $= 100\%$
Thus, 1000 metres is 100% of 1 km.
Question 98. Find out 8% of 25 kg.
Answer:
To find 8% of 25 kg, we can express 8% as a fraction or a decimal and then multiply by 25 kg.
Method 1: Convert Percentage to Fraction
$8\% = \frac{8}{100}$
So, 8% of 25 kg is:
$\frac{8}{100} \times 25 \text{ kg}$
Simplify the expression:
$\frac{8 \times 25}{100} \text{ kg}$
$\frac{200}{100} \text{ kg}$
$2 \text{ kg}$
Method 2: Convert Percentage to Decimal
$8\% = \frac{8}{100} = 0.08$
So, 8% of 25 kg is:
$0.08 \times 25 \text{ kg}$
Let's perform the multiplication:
$\begin{array}{cc}& & & 2 & 5 \\ \times & & 0 & . & 0 & 8 \\ \hline &&& 2 & 0 & 0 \\ & 0 & 0 & 0 & \times & \\ \hline &&& 2 & 0 & 0 \\ \hline \end{array}$
Since $0.08$ has two decimal places, the result will have two decimal places.
$0.08 \times 25 = 2.00$
Result $= 2.00 \text{ kg} = 2 \text{ kg}$
Using either method, the result is 2 kg.
Thus, 8% of 25 kg is 2 kg.
Question 99. What percent of ₹ 80 is ₹ 100?
Answer:
To find what percentage ₹100 is of ₹80, we need to calculate the ratio of ₹100 to ₹80 and express it as a percentage.
The required percentage is given by the formula:
Percentage $= \left(\frac{\text{Part}}{\text{Whole}}\right) \times 100\%$
Here, the 'Part' is $\textsf{₹} \text{ 100}$ and the 'Whole' is $\textsf{₹} \text{ 80}$.
Percentage $= \left(\frac{\textsf{₹} \text{ 100}}{\textsf{₹} \text{ 80}}\right) \times 100\%$
Percentage $= \frac{100}{80} \times 100\%$
Simplify the fraction $\frac{100}{80}$:
$\frac{100}{80} = \frac{10}{8} = \frac{5}{4}$
Now calculate the percentage:
Percentage $= \frac{5}{4} \times 100\%$
Percentage $= \frac{5 \times 100}{4}\%$
Percentage $= \frac{500}{4}\%$
Performing the division:
Percentage $= 125\%$
Thus, $\textsf{₹} \text{ 100}$ is 125% of $\textsf{₹} \text{ 80}$.
Question 100. 45% of the population of a town are men and 40% are women. What is the percentage of children?
Answer:
Let the total population of the town be 100%.
Given:
Percentage of men = 45%
Percentage of women = 40%
The population consists of men, women, and children. The sum of their percentages must equal 100%.
Percentage of men + Percentage of women + Percentage of children = 100%
We can find the combined percentage of men and women:
Combined percentage of adults (men and women) = Percentage of men + Percentage of women
Combined percentage of adults $= 45\% + 40\%$
Combined percentage of adults $= 85\%$
Now, we can find the percentage of children by subtracting the combined percentage of adults from the total percentage (100%).
Percentage of children = 100% - Combined percentage of adults
Percentage of children = 100% - 85%
Percentage of children = 15%
Thus, the percentage of children in the town is 15%.
Question 101. The strength of a school is 2000. If 40 % of the students are girls then how many boys are there in the school?
Answer:
Given:
Total strength of the school = 2000 students
Percentage of girls = 40%
To Find:
The number of boys in the school.
Solution:
The total percentage of students in the school is 100%.
The students consist of girls and boys.
Percentage of girls + Percentage of boys = 100%
We are given the percentage of girls, so we can find the percentage of boys:
Percentage of boys = 100% - Percentage of girls
Percentage of boys = $100\% - 40\%$
Percentage of boys = $60\%$
Now, we need to find the number of boys, which is 60% of the total strength.
Number of boys = 60% of 2000
Convert 60% to a fraction:
$60\% = \frac{60}{100}$
Number of boys $= \frac{60}{100} \times 2000$
Simplify the expression by cancelling the common factors:
Number of boys $= \frac{60}{\cancel{100}_{1}} \times \cancel{2000}^{20}$
Number of boys $= 60 \times 20$
Number of boys $= 1200$
Alternatively, we could calculate the number of girls first:
Number of girls = 40% of 2000
Number of girls $= \frac{40}{100} \times 2000$
Number of girls $= \frac{40}{\cancel{100}_{1}} \times \cancel{2000}^{20}$
Number of girls $= 40 \times 20 = 800$
Number of boys = Total strength - Number of girls
Number of boys $= 2000 - 800$
Number of boys $= 1200$
Both methods give the same result.
Thus, the number of boys in the school is 1200.
Question 102. Chalk contains 10% calcium, 3% carbon and 12% oxygen. Find the amount of carbon and calcium (in grams) in $2\frac{1}{2}$ kg of chalk.
Answer:
Given:
Percentage of calcium in chalk = 10%
Percentage of carbon in chalk = 3%
Total amount of chalk = $2\frac{1}{2}$ kg
To Find:
Amount of carbon and calcium (in grams) in $2\frac{1}{2}$ kg of chalk.
Solution:
First, convert the total amount of chalk from kilograms to grams.
$2\frac{1}{2} \text{ kg} = 2.5 \text{ kg}$
Since $1 \text{ kg} = 1000 \text{ g}$,
Total amount of chalk in grams $= 2.5 \times 1000 \text{ g} = 2500 \text{ g}$.
Now, we calculate the amount of calcium in 2500 g of chalk.
Amount of calcium = 10% of 2500 g
Amount of calcium $= \frac{10}{100} \times 2500 \text{ g}$
Amount of calcium $= \frac{\cancel{10}^{1}}{\cancel{100}_{10}} \times 2500 \text{ g}$
Amount of calcium $= \frac{1}{10} \times 2500 \text{ g}$
Amount of calcium $= \frac{\cancel{2500}^{250}}{\cancel{10}_{1}} \text{ g}$
Amount of calcium $= 250 \text{ g}$.
Next, we calculate the amount of carbon in 2500 g of chalk.
Amount of carbon = 3% of 2500 g
Amount of carbon $= \frac{3}{100} \times 2500 \text{ g}$
Amount of carbon $= \frac{3}{\cancel{100}_{1}} \times \cancel{2500}^{25} \text{ g}$
Amount of carbon $= 3 \times 25 \text{ g}$
Amount of carbon $= 75 \text{ g}$.
The amount of oxygen percentage is given, but not asked in the question.
Therefore, the amount of calcium in $2\frac{1}{2}$ kg of chalk is 250 g and the amount of carbon is 75 g.
Question 103. 800 kg of mortar consists of 55% sand, 33% cement and rest lime. What is the mass of lime in mortar?
Answer:
Given:
Total mass of mortar = 800 kg
Percentage of sand = 55%
Percentage of cement = 33%
The rest of the mortar is lime.
To Find:
The mass of lime in the mortar.
Solution:
The total percentage of the components in the mortar is 100%.
The components are sand, cement, and lime.
Percentage of sand + Percentage of cement + Percentage of lime = 100%
First, calculate the combined percentage of sand and cement:
Combined percentage of sand and cement $= 55\% + 33\%$
Combined percentage of sand and cement $= 88\%$
Now, find the percentage of lime:
Percentage of lime = 100% - (Percentage of sand + Percentage of cement)
Percentage of lime = $100\% - 88\%$
Percentage of lime = $12\%$
The mass of lime is 12% of the total mass of mortar (800 kg).
Mass of lime $= 12\%$ of 800 kg
Convert the percentage to a fraction:
$12\% = \frac{12}{100}$
Mass of lime $= \frac{12}{100} \times 800 \text{ kg}$
Simplify the expression by cancelling common factors:
Mass of lime $= \frac{12}{\cancel{100}_{1}} \times \cancel{800}^{8} \text{ kg}$
Mass of lime $= 12 \times 8 \text{ kg}$
Mass of lime $= 96 \text{ kg}$
Thus, the mass of lime in the mortar is 96 kg.
Question 104. In a furniture shop, 24 tables were bought at the rate of ₹ 450 per table. The shopkeeper sold 16 of them at the rate of ₹ 600 per table and the remaining at the rate of 400 per table. Find her gain or loss percent.
Answer:
Given:
Number of tables bought = 24
Cost Price per table = $\textsf{₹} \text{ 450}$
Number of tables sold at first rate = 16
Selling Price per table (for the first 16) = $\textsf{₹} \text{ 600}$
Number of remaining tables = $24 - 16 = 8$
Selling Price per table (for the remaining 8) = $\textsf{₹} \text{ 400}$
To Find:
Gain or Loss percent.
Solution:
First, calculate the total Cost Price (CP) of all 24 tables.
Total CP = Number of tables $\times$ Cost Price per table
Total CP $= 24 \times \textsf{₹} \text{ 450}$
$\begin{array}{cc}& & 4 & 5 & 0 \\ \times & & & 2 & 4 \\ \hline & 1 & 8 & 0 & 0 \\ & 9 & 0 & 0 & \times \\ \hline 1 & 0 & 8 & 0 & 0 \\ \hline \end{array}$
Total CP = $\textsf{₹} \text{ 10800}$.
Next, calculate the total Selling Price (SP) of all 24 tables. The tables were sold in two lots.
Selling Price of the first 16 tables = Number of tables $\times$ Selling Price per table
SP of 16 tables $= 16 \times \textsf{₹} \text{ 600}$
SP of 16 tables $= \textsf{₹} \text{ 9600}$.
Number of remaining tables $= 24 - 16 = 8$ tables.
Selling Price of the remaining 8 tables = Number of tables $\times$ Selling Price per table
SP of 8 tables $= 8 \times \textsf{₹} \text{ 400}$
SP of 8 tables $= \textsf{₹} \text{ 3200}$.
Total Selling Price (SP) = SP of 16 tables + SP of 8 tables
Total SP $= \textsf{₹} \text{ 9600} + \textsf{₹} \text{ 3200}$
$\begin{array}{cc} & 9 & 6 & 0 & 0 \\ + & 3 & 2 & 0 & 0 \\ \hline 1 & 2 & 8 & 0 & 0 \\ \hline \end{array}$
Total SP = $\textsf{₹} \text{ 12800}$.
Compare the Total Selling Price and Total Cost Price.
Total SP ($\textsf{₹} \text{ 12800}$) is greater than Total CP ($\textsf{₹} \text{ 10800}$).
This indicates a Gain.
Calculate the amount of Gain.
Gain = Total SP - Total CP
Gain $= \textsf{₹} \text{ 12800} - \textsf{₹} \text{ 10800}$
Gain $= \textsf{₹} \text{ 2000}$.
Calculate the Gain Percent.
Gain Percent $= \left(\frac{\text{Gain}}{\text{CP}}\right) \times 100\%$
Gain Percent $= \left(\frac{\textsf{₹} \text{ 2000}}{\textsf{₹} \text{ 10800}}\right) \times 100\%$
Gain Percent $= \frac{2000}{10800} \times 100\%$
Simplify the fraction:
Gain Percent $= \frac{20\cancel{00}}{108\cancel{00}} \times 100\%$
Gain Percent $= \frac{20}{108} \times 100\%$
Simplify $\frac{20}{108}$ by dividing numerator and denominator by 4:
$\frac{\cancel{20}^{5}}{\cancel{108}_{27}}$
Gain Percent $= \frac{5}{27} \times 100\%$
Gain Percent $= \frac{500}{27}\%$
To express this as a mixed number or decimal, perform the division $500 \div 27$.
$500 \div 27 = 18$ with a remainder of $500 - (27 \times 18) = 500 - 486 = 14$.
So, $\frac{500}{27} = 18\frac{14}{27}$.
Gain Percent $= 18\frac{14}{27}\%$.
As a decimal, $500 \div 27 \approx 18.5185...$
Gain Percent $\approx 18.52\%$ (rounded to two decimal places).
The question does not specify the format for the percentage, so the fraction or mixed number is accurate.
Thus, her gain percent is $18\frac{14}{27}\%$.
Question 105. Medha deposited 20% of her money in a bank. After spending 20% of the remainder, she has ₹ 4800 left with her. How much did she originally have?
Answer:
Given:
Percentage of money deposited in the bank = 20%
Percentage of remainder spent = 20%
Amount left after spending = $\textsf{₹} \text{ 4800}$
To Find:
The amount of money Medha originally had.
Solution:
Let the original amount of money Medha had be $\textsf{₹} \text{ } x$.
Amount deposited in the bank $= 20\%$ of $x$.
Amount deposited $= \frac{20}{100} \times x = \frac{1}{5}x$.
Amount remaining after depositing money $= \text{Original Amount} - \text{Amount Deposited}$.
Remainder $= x - \frac{1}{5}x = \frac{5x - x}{5} = \frac{4}{5}x$.
She spent 20% of this remainder ($\frac{4}{5}x$).
Amount spent $= 20\%$ of $\left(\frac{4}{5}x\right)$.
Amount spent $= \frac{20}{100} \times \frac{4}{5}x = \frac{1}{5} \times \frac{4}{5}x = \frac{4}{25}x$.
The amount left with her is the remainder minus the amount spent.
Amount left $= \text{Remainder} - \text{Amount Spent}$.
Amount left $= \frac{4}{5}x - \frac{4}{25}x$.
To subtract these fractions, find a common denominator, which is 25.
Amount left $= \frac{4 \times 5}{5 \times 5}x - \frac{4}{25}x = \frac{20}{25}x - \frac{4}{25}x = \frac{16}{25}x$.
We are given that the amount left is $\textsf{₹} \text{ 4800}$.
So, we can set up the equation:
$\frac{16}{25}x = 4800$
To solve for $x$, multiply both sides of the equation by the reciprocal of $\frac{16}{25}$, which is $\frac{25}{16}$.
$x = 4800 \times \frac{25}{16}$
Simplify the calculation by dividing 4800 by 16:
$\frac{4800}{16} = \frac{\cancel{4800}^{300}}{\cancel{16}_{1}} = 300$
Now, multiply the result by 25:
$x = 300 \times 25$
$\begin{array}{cc}& & 3 & 0 & 0 \\ \times & & & 2 & 5 \\ \hline & 1 & 5 & 0 & 0 \\ & 6 & 0 & 0 & \times \\ \hline 7 & 5 & 0 & 0 \\ \hline \end{array}$
$x = 7500$.
The original amount of money Medha had was $\textsf{₹} \text{ 7500}$.
Question 106. The cost of a flower vase got increased by 12%. If the current cost is ₹ 896, what was its original cost?
Answer:
Given:
Percentage increase in cost = 12%
Current cost (Increased cost) = $\textsf{₹} \text{ 896}$
To Find:
The original cost of the flower vase.
Solution:
Let the original cost of the flower vase be $\textsf{₹} \text{ } x$.
The cost increased by 12%.
The amount of increase $= 12\%$ of the original cost.
Increase amount $= 12\%$ of $x = \frac{12}{100} \times x = 0.12x$.
The current cost is the original cost plus the increase amount.
Current cost = Original cost + Increase amount
$\textsf{₹} \text{ 896} = x + 0.12x$
$896 = (1 + 0.12)x$
$896 = 1.12x$
To find $x$, divide 896 by 1.12.
$x = \frac{896}{1.12}$
To perform the division, remove the decimal from the denominator by multiplying both numerator and denominator by 100.
$x = \frac{896 \times 100}{1.12 \times 100}$
$x = \frac{89600}{112}$
Now, perform the division:
$89600 \div 112 = 800$
$\begin{array}{r} 800 \\ 112{\overline{\smash{\big)}\,89600}} \\ \underline{-~\phantom{(}896\phantom{00)}} \\ 000\phantom{)} \\ \underline{-~\phantom{()0}0\phantom{)}} \\ 0\phantom{)} \end{array}$
$x = 800$
The original cost of the flower vase was $\textsf{₹} \text{ 800}$.
Verification:
Original cost = $\textsf{₹} \text{ 800}$
Increase = 12% of $\textsf{₹} \text{ 800} = \frac{12}{100} \times 800 = 12 \times 8 = \textsf{₹} \text{ 96}$.
New cost = Original cost + Increase = $\textsf{₹} \text{ 800} + \textsf{₹} \text{ 96} = \textsf{₹} \text{ 896}$.
This matches the given current cost.
Thus, the original cost of the flower vase was $\textsf{₹} \text{ 800}$.
Question 107. Radhika borrowed ₹ 12000 from her friends. Out of which ₹ 4000 were borrowed at 18% and the remaining at 15% rate of interest per annum. What is the total interest after 3 years?
Answer:
Given:
Total amount borrowed = $\textsf{₹} \text{ 12000}$
Amount borrowed at 18% p.a. ($P_1$) = $\textsf{₹} \text{ 4000}$
Rate of interest for the first part ($R_1$) = 18% per annum
Time period for both parts ($T$) = 3 years
To Find:
The total interest after 3 years.
Solution:
First, find the remaining amount borrowed at 15% rate of interest.
Remaining amount ($P_2$) = Total amount borrowed - Amount borrowed at 18%
$P_2 = \textsf{₹} \text{ 12000} - \textsf{₹} \text{ 4000}$
$P_2 = \textsf{₹} \text{ 8000}$.
The rate of interest for this remaining amount ($R_2$) = 15% per annum.
Now, calculate the simple interest for the first part of the loan ($P_1 = \textsf{₹} \text{ 4000}$, $R_1 = 18\%$, $T = 3$ years).
The formula for Simple Interest (SI) is:
$SI = \frac{P \times R \times T}{100}$
Simple Interest for the first part ($SI_1$) $= \frac{P_1 \times R_1 \times T}{100}$
$SI_1 = \frac{4000 \times 18 \times 3}{100}$
Simplify the expression:
$SI_1 = \frac{40\cancel{00} \times 18 \times 3}{\cancel{100}_{1}}$
$SI_1 = 40 \times 18 \times 3$
$SI_1 = 40 \times 54$
$SI_1 = 2160$.
The simple interest for the first part is $\textsf{₹} \text{ 2160}$.
Next, calculate the simple interest for the second part of the loan ($P_2 = \textsf{₹} \text{ 8000}$, $R_2 = 15\%$, $T = 3$ years).
Simple Interest for the second part ($SI_2$) $= \frac{P_2 \times R_2 \times T}{100}$
$SI_2 = \frac{8000 \times 15 \times 3}{100}$
Simplify the expression:
$SI_2 = \frac{80\cancel{00} \times 15 \times 3}{\cancel{100}_{1}}$
$SI_2 = 80 \times 15 \times 3$
$SI_2 = 80 \times 45$
$SI_2 = 3600$.
The simple interest for the second part is $\textsf{₹} \text{ 3600}$.
Finally, calculate the total interest after 3 years.
Total Interest = $SI_1 + SI_2$
Total Interest $= \textsf{₹} \text{ 2160} + \textsf{₹} \text{ 3600}$
$\begin{array}{cc} & 2 & 1 & 6 & 0 \\ + & 3 & 6 & 0 & 0 \\ \hline & 5 & 7 & 6 & 0 \\ \hline \end{array}$
Total Interest = $\textsf{₹} \text{ 5760}$.
Thus, the total interest after 3 years is $\textsf{₹} \text{ 5760}$.
Question 108. A man travelled 60 km by car and 240 km by train. Find what per cent of total journey did he travel by car and what per cent by train?
Answer:
Given:
Distance travelled by car = 60 km
Distance travelled by train = 240 km
To Find:
Percentage of total journey by car and by train.
Solution:
First, calculate the total distance of the journey.
Total Distance = Distance by car + Distance by train
Total Distance $= 60 \text{ km} + 240 \text{ km} = 300 \text{ km}$.
Now, calculate the percentage of the journey travelled by car.
Percentage by car $= \left(\frac{\text{Distance by car}}{\text{Total Distance}}\right) \times 100\%$
Percentage by car $= \left(\frac{60 \text{ km}}{300 \text{ km}}\right) \times 100\%$
Percentage by car $= \frac{60}{300} \times 100\%$
Simplify the fraction $\frac{60}{300}$:
$\frac{60}{300} = \frac{\cancel{60}^{1}}{\cancel{300}_{5}} = \frac{1}{5}$
Percentage by car $= \frac{1}{5} \times 100\%$
Percentage by car $= \frac{100}{5}\% = 20\%$
The percentage of the total journey travelled by car is 20%.
Next, calculate the percentage of the journey travelled by train.
Percentage by train $= \left(\frac{\text{Distance by train}}{\text{Total Distance}}\right) \times 100\%$
Percentage by train $= \left(\frac{240 \text{ km}}{300 \text{ km}}\right) \times 100\%$
Percentage by train $= \frac{240}{300} \times 100\%$
Simplify the fraction $\frac{240}{300}$:
$\frac{240}{300} = \frac{\cancel{240}^{24}}{\cancel{300}_{30}} = \frac{\cancel{24}^{4}}{\cancel{30}_{5}} = \frac{4}{5}$
Percentage by train $= \frac{4}{5} \times 100\%$
Percentage by train $= \frac{400}{5}\% = 80\%$
Alternatively, since the journey is only by car and train, the percentages must add up to 100%.
Percentage by train = 100% - Percentage by car
Percentage by train $= 100\% - 20\% = 80\%$
The percentage of the total journey travelled by train is 80%.
Thus, the man travelled 20% of the total journey by car and 80% by train.
Question 109. By selling a chair for ₹ 1440, a shopkeeper loses 10%. At what price did he buy it?
Answer:
Given:
Selling Price (SP) of the chair = $\textsf{₹} \ 1440$
Loss percentage = $10\%$
To Find:
The price at which the shopkeeper bought the chair (Cost Price).
Solution:
Let the Cost Price (CP) of the chair be $\textsf{₹} \ CP$.
When an article is sold at a loss, the relationship between Selling Price (SP), Cost Price (CP), and Loss percent is given by the formula:
$SP = CP \times \left( \frac{100 - \text{Loss percent}}{100} \right)$
We can rearrange this formula to find the Cost Price:
$CP = \frac{SP \times 100}{100 - \text{Loss percent}}$
Now, substitute the given values into the formula:
$CP = \frac{1440 \times 100}{100 - 10}$
$CP = \frac{1440 \times 100}{90}$
$CP = \frac{144000}{90}$
$CP = \frac{14400}{9}$
Performing the division:
$CP = 1600$
Therefore, the Cost Price of the chair is $\textsf{₹} \ 1600$.
Answer: The shopkeeper bought the chair for $\textsf{₹} \ 1600$.
Question 110. Dhruvika invested money for a period from May 2006 to April 2008 at rate of 12% per annum. If interest received by her is ₹ 1620, find the money invested.
Answer:
Given:
Time period of investment = From May 2006 to April 2008
Rate of interest (R) = $12\%$ per annum
Simple Interest (SI) received = $\textsf{₹} \ 1620$
To Find:
The money invested (Principal, P).
Solution:
First, let's calculate the duration of the investment period in years.
The period from May 2006 to April 2008 covers:
Full year 1: May 2006 to April 2007 (1 year)
Full year 2: May 2007 to April 2008 (1 year)
Total time period (T) = $1 + 1 = 2$ years.
Alternatively, counting months:
2006: May to Dec (8 months)
2007: Jan to Dec (12 months)
2008: Jan to Apr (4 months)
Total months = $8 + 12 + 4 = 24$ months.
Time in years (T) = $\frac{24}{12} = 2$ years.
The formula for Simple Interest is:
$SI = \frac{P \times R \times T}{100}$
Where P is Principal, R is Rate, and T is Time.
We need to find the Principal (P). Rearranging the formula:
$P = \frac{SI \times 100}{R \times T}$
Substitute the given values:
$P = \frac{1620 \times 100}{12 \times 2}$
$P = \frac{162000}{24}$
Now, calculate the value of P:
$P = \frac{162000}{24} = 6750$
The money invested (Principal) is $\textsf{₹} \ 6750$.
Answer: The money invested by Dhruvika was $\textsf{₹} \ 6750$.
Question 111. A person wanted to sell a scooter at a loss of 25%. But at the last moment he changed his mind and sold the scooter at a loss of 20%. If the difference in the two SP’s is ₹ 4000, then find the CP of the scooter.
Answer:
Given:
Initial intended loss percentage = $25\%$
Actual loss percentage = $20\%$
Difference in the two Selling Prices = $\textsf{₹} \ 4000$
To Find:
The Cost Price (CP) of the scooter.
Solution:
Let the Cost Price of the scooter be $\textsf{₹} \ CP$.
The formula for Selling Price (SP) when there is a loss is:
$SP = CP \times \left( \frac{100 - \text{Loss percent}}{100} \right)$
Scenario 1: Intended sale at 25% loss
Intended Selling Price ($SP_1$) is:
$SP_1 = CP \times \left( \frac{100 - 25}{100} \right) = CP \times \frac{75}{100} = 0.75 \times CP$
Scenario 2: Actual sale at 20% loss
Actual Selling Price ($SP_2$) is:
$SP_2 = CP \times \left( \frac{100 - 20}{100} \right) = CP \times \frac{80}{100} = 0.80 \times CP$
The difference between the two Selling Prices is given as $\textsf{₹} \ 4000$. Since a smaller loss percentage results in a higher selling price, $SP_2$ is greater than $SP_1$.
$SP_2 - SP_1 = 4000$
Substitute the expressions for $SP_1$ and $SP_2$ in terms of $CP$:
$(0.80 \times CP) - (0.75 \times CP) = 4000$
$(0.80 - 0.75) \times CP = 4000$
$0.05 \times CP = 4000$
To find $CP$, divide the difference by $0.05$:
$CP = \frac{4000}{0.05}$
$CP = \frac{4000}{\frac{5}{100}} = \frac{4000 \times 100}{5}$
$CP = \frac{400000}{5}$
$CP = 80000$
The Cost Price of the scooter is $\textsf{₹} \ 80000$.
Answer: The Cost Price of the scooter is $\textsf{₹} \ 80000$.
Question 112. The population of a village is 8000. Out of these, 80% are literate and of these literate people, 40% are women. Find the ratio of the number of literate women to the total population.
Answer:
Given:
Total population of the village = $8000$
Percentage of literate people = $80\%$ of total population
Percentage of literate women = $40\%$ of literate people
To Find:
The ratio of the number of literate women to the total population.
Solution:
First, calculate the number of literate people in the village.
Number of literate people = $80\%$ of $8000$
Number of literate people = $\frac{80}{100} \times 8000$
Number of literate people = $0.80 \times 8000$
Number of literate people = $6400$
Next, calculate the number of literate women from the literate people.
Number of literate women = $40\%$ of the number of literate people
Number of literate women = $40\%$ of $6400$
Number of literate women = $\frac{40}{100} \times 6400$
Number of literate women = $0.40 \times 6400$
Number of literate women = $2560$
Now, find the ratio of the number of literate women to the total population.
Ratio = $\frac{\text{Number of literate women}}{\text{Total population}}$
Ratio = $\frac{2560}{8000}$
Simplify the fraction:
Ratio = $\frac{256}{800}$ (Dividing both numerator and denominator by 10)
Divide both by 16:
$\frac{256 \div 16}{800 \div 16} = \frac{16}{50}$
Divide both by 2:
$\frac{16 \div 2}{50 \div 2} = \frac{8}{25}$
The ratio is $8:25$.
Answer: The ratio of the number of literate women to the total population is $8:25$.
Question 113. In an entertainment programme, 250 tickets of ₹ 400 and 500 tickets of ₹ 100 were sold. If the entertainment tax is 40% on ticket of ₹ 400 and 20% on ticket of ₹ 100, find how much entertainment tax was collected from the programme.
Answer:
Given:
Number of tickets of $\textsf{₹} \ 400$ sold = $250$
Entertainment tax on $\textsf{₹} \ 400$ tickets = $40\%$
Number of tickets of $\textsf{₹} \ 100$ sold = $500$
Entertainment tax on $\textsf{₹} \ 100$ tickets = $20\%$
To Find:
Total entertainment tax collected from the programme.
Solution:
First, calculate the entertainment tax collected from the tickets of $\textsf{₹} \ 400$.
Tax per $\textsf{₹} \ 400$ ticket = $40\%$ of $\textsf{₹} \ 400$
Tax per $\textsf{₹} \ 400$ ticket = $\frac{40}{100} \times 400 = 0.40 \times 400 = \textsf{₹} \ 160$
Total tax from $\textsf{₹} \ 400$ tickets = Number of tickets $\times$ Tax per ticket
Total tax from $\textsf{₹} \ 400$ tickets = $250 \times 160$
Total tax from $\textsf{₹} \ 400$ tickets = $\textsf{₹} \ 40000$
Next, calculate the entertainment tax collected from the tickets of $\textsf{₹} \ 100$.
Tax per $\textsf{₹} \ 100$ ticket = $20\%$ of $\textsf{₹} \ 100$
Tax per $\textsf{₹} \ 100$ ticket = $\frac{20}{100} \times 100 = 0.20 \times 100 = \textsf{₹} \ 20$
Total tax from $\textsf{₹} \ 100$ tickets = Number of tickets $\times$ Tax per ticket
Total tax from $\textsf{₹} \ 100$ tickets = $500 \times 20$
Total tax from $\textsf{₹} \ 100$ tickets = $\textsf{₹} \ 10000$
Finally, calculate the total entertainment tax collected from the programme.
Total entertainment tax = Tax from $\textsf{₹} \ 400$ tickets + Tax from $\textsf{₹} \ 100$ tickets
Total entertainment tax = $\textsf{₹} \ 40000 + \textsf{₹} \ 10000$
Total entertainment tax = $\textsf{₹} \ 50000$
Answer: The total entertainment tax collected from the programme was $\textsf{₹} \ 50000$.
Question 114. Bhavya earns ₹ 50,000 per month and spends 80% of it. Due to pay revision, her monthly income increases by 20% but due to price rise, she has to spend 20% more. Find her new savings.
Answer:
Given:
Initial monthly income = $\textsf{₹} \ 50000$
Initial spending percentage = $80\%$ of initial income
Increase in monthly income = $20\%$
Increase in spending = $20\%$ of initial spending
To Find:
Her new savings.
Solution:
First, calculate her initial spending.
Initial spending = $80\%$ of $\textsf{₹} \ 50000$
Initial spending = $\frac{80}{100} \times 50000 = 0.80 \times 50000 = \textsf{₹} \ 40000$
Initial savings = Initial income - Initial spending
Initial savings = $\textsf{₹} \ 50000 - \textsf{₹} \ 40000 = \textsf{₹} \ 10000$
Now, calculate her new monthly income after the $20\%$ increase.
Increase in income = $20\%$ of $\textsf{₹} \ 50000$
Increase in income = $\frac{20}{100} \times 50000 = 0.20 \times 50000 = \textsf{₹} \ 10000$
New income = Initial income + Increase in income
New income = $\textsf{₹} \ 50000 + \textsf{₹} \ 10000 = \textsf{₹} \ 60000$
Next, calculate her new spending after the $20\%$ increase in spending.
Increase in spending amount = $20\%$ of initial spending
Increase in spending amount = $20\%$ of $\textsf{₹} \ 40000$
Increase in spending amount = $\frac{20}{100} \times 40000 = 0.20 \times 40000 = \textsf{₹} \ 8000$
New spending = Initial spending + Increase in spending amount
New spending = $\textsf{₹} \ 40000 + \textsf{₹} \ 8000 = \textsf{₹} \ 48000$
Finally, calculate her new savings.
New savings = New income - New spending
New savings = $\textsf{₹} \ 60000 - \textsf{₹} \ 48000 = \textsf{₹} \ 12000$
Answer: Her new savings are $\textsf{₹} \ 12000$.
Question 115. In an examination, there are three papers each of 100 marks. A candidate obtained 53 marks in the first and 75 marks in the second paper. How many marks must the candidate obtain in the third paper to get an overall of 70 per cent marks?
Answer:
Given:
Number of papers = $3$
Maximum marks for each paper = $100$
Marks obtained in the first paper = $53$
Marks obtained in the second paper = $75$
Target overall percentage = $70\%$
To Find:
Marks the candidate must obtain in the third paper.
Solution:
First, calculate the total maximum marks for the examination.
Total maximum marks = Number of papers $\times$ Maximum marks per paper
Total maximum marks = $3 \times 100 = 300$
Next, calculate the total marks required to achieve an overall of $70\%$.
Target total marks = $70\%$ of Total maximum marks
Target total marks = $\frac{70}{100} \times 300$
Target total marks = $0.70 \times 300 = 210$
Let $x$ be the marks obtained by the candidate in the third paper.
The total marks obtained by the candidate is the sum of marks in all three papers.
Total marks obtained = Marks in Paper 1 + Marks in Paper 2 + Marks in Paper 3
Total marks obtained = $53 + 75 + x$
We know that the total marks obtained must be equal to the target total marks to achieve $70\%$.
$53 + 75 + x = 210$
Add the marks obtained in the first two papers:
$53 + 75 = 128$
So, the equation becomes:
$128 + x = 210$
Now, solve for $x$ by subtracting $128$ from both sides of the equation:
$x = 210 - 128$
$x = 82$
The candidate must obtain $82$ marks in the third paper.
Answer: The candidate must obtain $82$ marks in the third paper to get an overall of $70$ per cent marks.
Question 116. Health Application
A doctor reports blood pressure in millimetres of mercury (mm Hg) as a ratio of systolic blood pressure to diastolic blood pressure (such as 140 over 80). Systolic pressure is measured when the heart beats, and diastolic pressure is measured when it rests. Refer to the table of blood pressure ranges for adults.
| Blood Pressure Rane | |||
|---|---|---|---|
| Normal | Prehypertension | Hypertension (Very High) | |
| Sytolic | Under 120 mm Hg | 120 - 139 mm Hg | 140 mm Hg and above |
| Distolic | Under 80 mm Hg | 80 - 89 mm Hg | 90 mm Hg and above |
Manohar is a healthy 37 years old man whose blood pressure is in the normal category.
(a) Calculate an approximate ratio of systolic to diastolic blood pressures in the normal range.
(b) If Manohar’s systolic blood pressure is 102 mm Hg, use the ratio from part (a) to predict his diastolic blood pressure.
(c) Calculate ratio of average systolic to average diastolic blood pressure in the prehypertension category.
Answer:
Given:
Blood pressure table ranges for adults is provided.
Manohar's blood pressure is in the normal category.
To Find:
(a) Approximate ratio of systolic to diastolic blood pressures in the normal range.
(b) Predict Manohar's diastolic blood pressure if his systolic pressure is $102$ mm Hg, using the ratio from part (a).
(c) Ratio of average systolic to average diastolic blood pressure in the prehypertension category.
Solution:
Part (a)
From the table, the normal range is:
Systolic: Under $120$ mm Hg
Diastolic: Under $80$ mm Hg
To find an approximate ratio, we can consider typical values within this normal range. Common healthy blood pressure readings are around $110/70$ or $115/75$. Let's use $110$ for systolic and $70$ for diastolic as representative values within the 'Under' range.
Approximate ratio $\frac{\text{Systolic}}{\text{Diastolic}} = \frac{110}{70}$
Simplify the ratio:
$\frac{110}{70} = \frac{11}{7}$
The approximate ratio of systolic to diastolic blood pressures in the normal range is $\frac{11}{7}$.
Part (b)
Manohar's systolic blood pressure is $102$ mm Hg.
Using the approximate ratio from part (a), which is $\frac{11}{7}$, we can set up the proportion:
$\frac{\text{Systolic}}{\text{Diastolic}} = \frac{11}{7}$
Substitute Manohar's systolic pressure ($102$) into the equation:
$\frac{102}{\text{Diastolic}} = \frac{11}{7}$
To find the diastolic pressure, rearrange the equation:
$\text{Diastolic} = \frac{102 \times 7}{11}$
Calculate the value:
$102 \times 7 = 714$
$\text{Diastolic} = \frac{714}{11}$
Performing the division:
$\frac{714}{11} \approx 64.91$ mm Hg
Predicting Manohar's diastolic blood pressure using the approximate ratio gives a value around $64.9$ mm Hg.
Part (c)
From the table, the prehypertension range is:
Systolic: $120 - 139$ mm Hg
Diastolic: $80 - 89$ mm Hg
Calculate the average systolic blood pressure in this range:
Average Systolic = $\frac{120 + 139}{2} = \frac{259}{2} = 129.5$ mm Hg
Calculate the average diastolic blood pressure in this range:
Average Diastolic = $\frac{80 + 89}{2} = \frac{169}{2} = 84.5$ mm Hg
Calculate the ratio of average systolic to average diastolic blood pressure:
Ratio = $\frac{\text{Average Systolic}}{\text{Average Diastolic}} = \frac{129.5}{84.5}$
To simplify the ratio, multiply the numerator and denominator by 10 to remove the decimal:
Ratio = $\frac{1295}{845}$
Both numbers end in 5, so they are divisible by 5:
$\frac{1295 \div 5}{845 \div 5} = \frac{259}{169}$
Recognize that $169 = 13^2$. Check if $259$ is divisible by 13:
$259 = 13 \times 19$
So, simplify the fraction by dividing both by 13:
$\frac{259 \div 13}{169 \div 13} = \frac{19}{13}$
The ratio of average systolic to average diastolic blood pressure in the prehypertension category is $\frac{19}{13}$.
Answer:
(a) The approximate ratio of systolic to diastolic blood pressures in the normal range is $\frac{11}{7}$.
(b) If Manohar’s systolic blood pressure is $102$ mm Hg, his predicted diastolic blood pressure is approximately $64.9$ mm Hg.
(c) The ratio of average systolic to average diastolic blood pressure in the prehypertension category is $\frac{19}{13}$.
Question 117.
(a) Science Application: The king cobra can reach a length of 558 cm. This is only about 60 per cent of the length of the largest reticulated python. Find the length of the largest reticulated python.
(b) Physical Science Application: Unequal masses will not balance on a fulcrum if they are at equal distance from it; one side will go up and the other side will go down. Unequal masses will balance when the following proportion is true:
$\frac{mass\;1}{length\;2} = \frac{mass\;2}{length\;1}$

Two children can be balanced on a seesaw when $\frac{mass\;1}{length\;2} = \frac{mass\;2}{length\;1}$ . The child on the left and child on the right are balanced. What is the mass of the child on the right?
(c) Life Science Application
A DNA model was built using the scale 2 cm : 0.0000001 mm. If the model of the DNA chain is 17 cm long, what is the length of the actual chain?
Answer:
Given:
(a) King cobra length = $558$ cm, which is $60\%$ of the largest reticulated python length.
(b) Seesaw balance proportion: $\frac{mass\;1}{length\;2} = \frac{mass\;2}{length\;1}$. Mass 1 = $25$ kg, Length 1 = $1.6$ m, Length 2 = $2.5$ m.
(c) DNA model scale: $2$ cm (model) : $0.0000001$ mm (actual). Model length = $17$ cm.
To Find:
(a) The length of the largest reticulated python.
(b) The mass of the child on the right (Mass 2).
(c) The length of the actual DNA chain.
Solution:
Part (a)
Let the length of the largest reticulated python be $L_p$ cm.
According to the problem, the king cobra's length ($558$ cm) is $60\%$ of $L_p$.
$60\%$ of $L_p = 558$
Write the percentage as a fraction:
$\frac{60}{100} \times L_p = 558$
$0.60 \times L_p = 558$
Solve for $L_p$:
$L_p = \frac{558}{0.60}$
$L_p = \frac{558}{\frac{60}{100}} = \frac{558 \times 100}{60}$
$L_p = \frac{55800}{60}$
$L_p = \frac{5580}{6}$
$L_p = 930$
The length of the largest reticulated python is $930$ cm.
Part (b)
The balance condition for the seesaw is given by the proportion:
$\frac{mass\;1}{length\;2} = \frac{mass\;2}{length\;1}$
From the image, we have:
Mass 1 (child on left) = $25$ kg
Length 1 (distance of child 1 from fulcrum) = $1.6$ m
Length 2 (distance of child 2 from fulcrum) = $2.5$ m
Mass 2 (child on right) = $M_2$ kg (what we need to find)
Substitute these values into the proportion:
$\frac{25}{2.5} = \frac{M_2}{1.6}$
Now, solve for $M_2$:
$M_2 = \frac{25}{2.5} \times 1.6$
$\frac{25}{2.5} = \frac{250}{25} = 10$
$M_2 = 10 \times 1.6$
$M_2 = 16$
The mass of the child on the right is $16$ kg.
Part (c)
The scale is given as $2$ cm (model) : $0.0000001$ mm (actual).
This means that every $2$ cm on the model represents $0.0000001$ mm of the actual DNA chain.
We can set up a proportion:
$\frac{\text{Model Length}}{\text{Actual Length}} = \frac{2 \text{ cm}}{0.0000001 \text{ mm}}$
We are given the model length is $17$ cm. Let the actual length be $L_a$ mm.
$\frac{17 \text{ cm}}{L_a \text{ mm}} = \frac{2 \text{ cm}}{0.0000001 \text{ mm}}$
Cross-multiply:
$17 \times 0.0000001 = 2 \times L_a$
$0.0000017 = 2 \times L_a$
Solve for $L_a$:
$L_a = \frac{0.0000017}{2}$
$L_a = 0.00000085$ mm
We can express this length in scientific notation or other units for clarity.
$0.00000085$ mm $= 8.5 \times 10^{-7}$ mm.
To convert to nanometers (nm), recall that $1$ mm $= 10^6$ nm:
$L_a = 8.5 \times 10^{-7} \text{ mm} \times \frac{10^6 \text{ nm}}{1 \text{ mm}}$
$L_a = 8.5 \times 10^{-7} \times 10^6$ nm
$L_a = 8.5 \times 10^{-1}$ nm
$L_a = 0.85$ nm
The length of the actual DNA chain is $0.00000085$ mm or $0.85$ nm.
Answer:
(a) The length of the largest reticulated python is $930$ cm.
(b) The mass of the child on the right is $16$ kg.
(c) The length of the actual DNA chain is $0.00000085$ mm (or $0.85$ nm).
Question 118. Language Application
Given below are few Mathematical terms.

Find
(a) The ratio of consonants to vowels in each of the terms.
(b) The percentage of consonants in each of the terms.
Answer:
Given:
List of Mathematical terms from the image.
To Find:
(a) The ratio of consonants to vowels in each term.
(b) The percentage of consonants in each term.
Solution:
We will count the number of vowels (A, E, I, O, U) and consonants in each term to find the ratio and percentage.
Total letters = Number of Vowels + Number of Consonants.
Ratio of Consonants to Vowels = Consonants : Vowels.
Percentage of Consonants = $\left(\frac{\text{Number of Consonants}}{\text{Total letters}}\right) \times 100\%$.
Here is the analysis for each term:
| Term | Vowels | Consonants | Total Letters | Ratio (C:V) | Percentage of Consonants |
| AVERAGE | 4 (A, E, A, E) | 3 (V, R, G) | 7 | $3:4$ | $\frac{3}{7} \times 100\% \approx 42.86\%$ |
| RATIO | 3 (A, I, O) | 2 (R, T) | 5 | $2:3$ | $\frac{2}{5} \times 100\% = 40\%$ |
| PERCENTAGE | 4 (E, E, A, E) | 6 (P, R, C, N, T, G) | 10 | $6:4 = 3:2$ | $\frac{6}{10} \times 100\% = 60\%$ |
| DECIMAL | 3 (E, I, A) | 4 (D, C, M, L) | 7 | $4:3$ | $\frac{4}{7} \times 100\% \approx 57.14\%$ |
| FRACTION | 3 (A, I, O) | 5 (F, R, C, T, N) | 8 | $5:3$ | $\frac{5}{8} \times 100\% = 62.5\%$ |
| SIMPLE | 2 (I, E) | 4 (S, M, P, L) | 6 | $4:2 = 2:1$ | $\frac{4}{6} \times 100\% = \frac{2}{3} \times 100\% \approx 66.67\%$ |
| PROFIT | 2 (O, I) | 4 (P, R, F, T) | 6 | $4:2 = 2:1$ | $\frac{4}{6} \times 100\% = \frac{2}{3} \times 100\% \approx 66.67\%$ |
| LOSS | 1 (O) | 3 (L, S, S) | 4 | $3:1$ | $\frac{3}{4} \times 100\% = 75\%$ |
| INTEREST | 3 (I, E, E) | 5 (N, T, R, S, T) | 8 | $5:3$ | $\frac{5}{8} \times 100\% = 62.5\%$ |
| AMOUNT | 3 (A, O, U) | 3 (M, N, T) | 6 | $3:3 = 1:1$ | $\frac{3}{6} \times 100\% = 50\%$ |
| PRINCIPAL | 3 (I, I, A) | 6 (P, R, N, C, P, L) | 9 | $6:3 = 2:1$ | $\frac{6}{9} \times 100\% = \frac{2}{3} \times 100\% \approx 66.67\%$ |
| RATE | 2 (A, E) | 2 (R, T) | 4 | $2:2 = 1:1$ | $\frac{2}{4} \times 100\% = 50\%$ |
| TIME | 2 (I, E) | 2 (T, M) | 4 | $2:2 = 1:1$ | $\frac{2}{4} \times 100\% = 50\%$ |
Answer:
(a) The ratio of consonants to vowels for each term is given in the 'Ratio (C:V)' column of the table above.
(b) The percentage of consonants for each term is given in the 'Percentage of Consonants' column of the table above.
Question 119. What’s the Error? An analysis showed that 0.06 per cent of the T-shirts made by one company were defective. A student says this is 6 out of every 100. What is the student’s error?
Answer:
Given:
Percentage of defective T-shirts = $0.06\%$
Student's statement: This is $6$ out of every $100$.
To Find:
The student's error.
Solution:
The percentage $0.06\%$ means $0.06$ per $100$.
To express this as a fraction, we write:
$0.06\% = \frac{0.06}{100}$
To remove the decimal point from the numerator, we can multiply both the numerator and the denominator by $100$:
$\frac{0.06 \times 100}{100 \times 100} = \frac{6}{10000}$
This fraction $\frac{6}{10000}$ means $6$ out of every $10000$ T-shirts are defective.
The student's statement is that $0.06\%$ is $6$ out of every $100$. This corresponds to the fraction $\frac{6}{100}$.
The fraction $\frac{6}{100}$ represents $6\%$, not $0.06\%$.
The student confused $0.06\%$ with $6\%$.
Explanation of the error:
The student incorrectly interpreted $0.06\%$ as $6\%$.
$0.06\%$ means $\frac{0.06}{100}$, which is equivalent to $\frac{6}{10000}$.
$6\%$ means $\frac{6}{100}$.
So, $0.06\%$ is $6$ out of every $10000$, not $6$ out of every $100$. The student's value is $100$ times larger than the correct value.
Answer: The student's error is confusing $0.06\%$ with $6\%$. $0.06\%$ means $6$ out of every $10000$ T-shirts, not $6$ out of every $100$ T-shirts.
Question 120. What’s the Error? A student said that the ratios $\frac{3}{4}$ and $\frac{9}{16}$ were proportional. What error did the student make?
Answer:
Given:
Ratio 1 = $\frac{3}{4}$
Ratio 2 = $\frac{9}{16}$
Student's statement: The ratios $\frac{3}{4}$ and $\frac{9}{16}$ are proportional.
To Find:
The student's error.
Solution:
Two ratios are proportional if they are equivalent, meaning they represent the same value. In other words, if $\frac{a}{b}$ and $\frac{c}{d}$ are proportional, then $\frac{a}{b} = \frac{c}{d}$. This can be checked by cross-multiplication ($a \times d = b \times c$) or by simplifying the fractions to their lowest terms.
Let's check if the ratios $\frac{3}{4}$ and $\frac{9}{16}$ are equivalent.
Method 1: Cross-multiplication
We check if $3 \times 16$ is equal to $4 \times 9$.
$3 \times 16 = 48$
$4 \times 9 = 36$
Since $48 \neq 36$, the ratios are not proportional.
Method 2: Simplifying the fractions
The fraction $\frac{3}{4}$ is already in its simplest form.
The fraction $\frac{9}{16}$ is also in its simplest form (the greatest common divisor of 9 and 16 is 1).
Since the simplest forms of the two ratios are not equal ($\frac{3}{4} \neq \frac{9}{16}$), the ratios are not proportional.
Alternatively, we can try to make the denominators the same:
Multiply the numerator and denominator of the first ratio by $4$ to get a denominator of $16$:
$\frac{3}{4} = \frac{3 \times 4}{4 \times 4} = \frac{12}{16}$
Now we compare $\frac{12}{16}$ and $\frac{9}{16}$.
Since $12 \neq 9$, $\frac{12}{16} \neq \frac{9}{16}$.
So, the ratios $\frac{3}{4}$ and $\frac{9}{16}$ are not proportional.
Explanation of the error:
The student incorrectly concluded that the ratios $\frac{3}{4}$ and $\frac{9}{16}$ are proportional. The error lies in not correctly checking for the equivalence of the two ratios. Two ratios are proportional only if they are equal fractions. The student might have simply observed that $9$ is a multiple of $3$ and $16$ is a multiple of $4$, but this does not guarantee proportionality unless the multiplier is the same for both the numerator and the denominator when going from one ratio to the other. In this case, to get from $3$ to $9$, you multiply by $3$. To get from $4$ to $16$, you multiply by $4$. Since the multipliers are different ($3 \neq 4$), the ratios are not equivalent and thus not proportional.
Answer: The student's error was stating that the ratios were proportional without verifying that they were equivalent fractions. The ratios $\frac{3}{4}$ and $\frac{9}{16}$ are not equal, and therefore not proportional.
Question 121. What’s the Error? A clothing store charges ₹ 1024 for 4 T-shirts. A student says that the unit price is ₹ 25.6 per T-shirt. What is the error? What is the correct unit price?
Answer:
Given:
Cost of 4 T-shirts = $\textsf{₹} \ 1024$
Student's claimed unit price = $\textsf{₹} \ 25.6$ per T-shirt
To Find:
The student's error and the correct unit price.
Solution:
The unit price is the cost per item. To find the unit price, we need to divide the total cost by the number of items.
Correct Unit Price = $\frac{\text{Total Cost}}{\text{Number of T-shirts}}$
Correct Unit Price = $\frac{\textsf{₹} \ 1024}{4}$
Performing the division:
$1024 \div 4 = 256$
So, the correct unit price is $\textsf{₹} \ 256$ per T-shirt.
The student stated that the unit price is $\textsf{₹} \ 25.6$.
Comparing the student's price ($\textsf{₹} \ 25.6$) with the correct price ($\textsf{₹} \ 256$), we see that they are different.
The student's value is $25.6$, while the correct value is $256$. The student's value is exactly one-tenth of the correct value ($256 \div 10 = 25.6$).
The error is a mistake in calculating the unit price. The student likely made an error in the division or misplaced the decimal point.
Answer:
The student's error is in the calculation of the unit price. The student incorrectly calculated $\textsf{₹} \ 1024 \div 4$ as $\textsf{₹} \ 25.6$.
The correct unit price is $\textsf{₹} \ 256$ per T-shirt.
Question 122. A tea merchant blends two varieties of tea in the ratio of 5 : 4. The cost of first variety is ₹ 200 per kg and that of second variety is ₹ 300 per kg. If he sells the blended tea at the rate of ₹ 275 per kg, find out the percentage of her profit or loss.
Answer:
Given:
Ratio of blending two varieties of tea = $5:4$
Cost of first variety = $\textsf{₹} \ 200$ per kg
Cost of second variety = $\textsf{₹} \ 300$ per kg
Selling price of blended tea = $\textsf{₹} \ 275$ per kg
To Find:
The percentage of profit or loss.
Solution:
Let's assume the merchant blends $5$ kg of the first variety and $4$ kg of the second variety, as per the given ratio $5:4$.
Cost of $5$ kg of the first variety = $5 \text{ kg} \times \textsf{₹} \ 200 \text{/kg} = \textsf{₹} \ 1000$
Cost of $4$ kg of the second variety = $4 \text{ kg} \times \textsf{₹} \ 300 \text{/kg} = \textsf{₹} \ 1200$
Total weight of the blended tea = $5 \text{ kg} + 4 \text{ kg} = 9$ kg
Total Cost Price (CP) of $9$ kg of blended tea = Cost of variety 1 + Cost of variety 2
Total CP = $\textsf{₹} \ 1000 + \textsf{₹} \ 1200 = \textsf{₹} \ 2200$
The merchant sells the blended tea at $\textsf{₹} \ 275$ per kg.
Total Selling Price (SP) of $9$ kg of blended tea = $9 \text{ kg} \times \textsf{₹} \ 275 \text{/kg}$
Total SP = $9 \times 275 = \textsf{₹} \ 2475$
Now, compare the Total SP and Total CP.
Total SP ($\textsf{₹} \ 2475$) is greater than Total CP ($\textsf{₹} \ 2200$). Therefore, there is a profit.
Profit = Total SP - Total CP
Profit = $\textsf{₹} \ 2475 - \textsf{₹} \ 2200 = \textsf{₹} \ 275$
Calculate the profit percentage:
Profit Percentage = $\left( \frac{\text{Profit}}{\text{CP}} \right) \times 100\%$
Profit Percentage = $\left( \frac{275}{2200} \right) \times 100\%$
Simplify the fraction $\frac{275}{2200}$. Both numerator and denominator are divisible by 25.
$\frac{275}{25} = 11$
$\frac{2200}{25} = 88$
So, the fraction is $\frac{11}{88}$. This can be simplified further by dividing by 11.
$\frac{11 \div 11}{88 \div 11} = \frac{1}{8}$
Profit Percentage = $\frac{1}{8} \times 100\%$
Profit Percentage = $\frac{100}{8}\%$
Profit Percentage = $12.5\%$
Answer: The merchant makes a profit of $12.5\%$.
Question 123. A piece of cloth 5 m long shrinks 10 per cent on washing. How long will the cloth be after washing?
Answer:
Given:
Original length of the cloth = $5$ m
Percentage of shrinkage on washing = $10\%$
To Find:
The length of the cloth after washing.
Solution:
First, calculate the amount of shrinkage in length.
Shrinkage amount = $10\%$ of the original length
Shrinkage amount = $10\%$ of $5$ m
Shrinkage amount = $\frac{10}{100} \times 5$ m
Shrinkage amount = $0.10 \times 5$ m
Shrinkage amount = $0.5$ m
Now, subtract the shrinkage amount from the original length to find the length after washing.
Length after washing = Original length - Shrinkage amount
Length after washing = $5$ m - $0.5$ m
Length after washing = $4.5$ m
Alternatively, if $10\%$ of the cloth shrinks, then $(100 - 10)\% = 90\%$ of the original length remains.
Length after washing = $90\%$ of original length
Length after washing = $90\%$ of $5$ m
Length after washing = $\frac{90}{100} \times 5$ m
Length after washing = $0.90 \times 5$ m
Length after washing = $4.5$ m
Answer: The cloth will be $4.5$ m long after washing.
Question 124. Nancy obtained 426 marks out of 600 and the marks obtained by Rohit are 560 out of 800. Whose performance is better?
Answer:
Given:
Nancy's marks obtained = $426$ out of $600$ total marks.
Rohit's marks obtained = $560$ out of $800$ total marks.
To Find:
Whose performance is better.
Solution:
To compare the performance of Nancy and Rohit, we need to calculate the percentage of marks obtained by each student.
The formula for percentage of marks is:
Percentage of Marks = $\left( \frac{\text{Marks Obtained}}{\text{Total Marks}} \right) \times 100\%$
Calculate Nancy's percentage of marks:
Nancy's Percentage = $\left( \frac{426}{600} \right) \times 100\%$
Nancy's Percentage = $\frac{426}{6} \%$
Nancy's Percentage = $71\%$
Calculate Rohit's percentage of marks:
Rohit's Percentage = $\left( \frac{560}{800} \right) \times 100\%$
Rohit's Percentage = $\frac{560}{8} \%$
Rohit's Percentage = $70\%$
Now, compare the percentages obtained by Nancy and Rohit.
Nancy's Percentage = $71\%$
Rohit's Percentage = $70\%$
Since $71\% > 70\%$, Nancy's performance is better than Rohit's performance.
Answer: Nancy's performance is better.
Question 125. A memorial trust donates ₹ 5,00,000 to a school, the interest on which is to be used for awarding 3 scholarships to students obtaining first three positions in the school examination every year. If the donation earns an interest of 12 per cent per annum and the values of the second and third scholarships are ₹ 20,000 and ₹ 15,000 respectively, find out the value of the first scholarship.
Answer:
Given:
Donation amount (Principal, P) = $\textsf{₹} \ 5,00,000$
Rate of interest (R) = $12\%$ per annum
Number of scholarships = $3$
Value of second scholarship = $\textsf{₹} \ 20,000$
Value of third scholarship = $\textsf{₹} \ 15,000$
Time period (for calculating annual interest, T) = $1$ year
To Find:
The value of the first scholarship.
Solution:
First, calculate the total interest earned by the donation in one year. This total interest is used to fund the three scholarships.
Using the Simple Interest formula: $SI = \frac{P \times R \times T}{100}$
$SI = \frac{500000 \times 12 \times 1}{100}$
$SI = \frac{5000 \times 12 \times 1}{1}$
$SI = 5000 \times 12$
$SI = 60000$
The total annual interest earned is $\textsf{₹} \ 60,000$.
This total interest is distributed as the three scholarships. Let the value of the first scholarship be $\textsf{₹} \ S_1$.
Total Annual Interest = Value of 1st Scholarship + Value of 2nd Scholarship + Value of 3rd Scholarship
$60000 = S_1 + 20000 + 15000$
Combine the known scholarship values:
$20000 + 15000 = 35000$
So, the equation becomes:
$60000 = S_1 + 35000$
Now, solve for $S_1$ by subtracting $35000$ from both sides of the equation:
$S_1 = 60000 - 35000$
$S_1 = 25000$
The value of the first scholarship is $\textsf{₹} \ 25,000$.
Answer: The value of the first scholarship is $\textsf{₹} \ 25,000$.
Question 126. Ambika got 99 per cent marks in Mathematics, 76 per cent marks in Hindi, 61 per cent in English, 84 per cent in Science, and 95% in Social Science. If each subject carries 100 marks, then find the percentage of marks obtained by Ambika in the aggregate of all the subjects.
Answer:
Given:
Marks obtained in Mathematics = $99\%$
Marks obtained in Hindi = $76\%$
Marks obtained in English = $61\%$
Marks obtained in Science = $84\%$
Marks obtained in Social Science = $95\%$
Maximum marks for each subject = $100$
To Find:
The percentage of marks obtained by Ambika in the aggregate of all the subjects.
Solution:
Since each subject carries $100$ marks, the percentage of marks obtained in each subject is equal to the marks obtained in that subject.
Marks in Mathematics = $99$ marks
Marks in Hindi = $76$ marks
Marks in English = $61$ marks
Marks in Science = $84$ marks
Marks in Social Science = $95$ marks
Calculate the total marks obtained by Ambika:
Total Marks Obtained = $99 + 76 + 61 + 84 + 95$
Total Marks Obtained = $415$
Calculate the total maximum marks for all subjects:
Number of subjects = $5$
Total Maximum Marks = Number of subjects $\times$ Maximum marks per subject
Total Maximum Marks = $5 \times 100 = 500$
Now, calculate the aggregate percentage of marks obtained by Ambika.
Aggregate Percentage = $\left( \frac{\text{Total Marks Obtained}}{\text{Total Maximum Marks}} \right) \times 100\%$
Aggregate Percentage = $\left( \frac{415}{500} \right) \times 100\%$
Aggregate Percentage = $\frac{415}{5}\%$
Aggregate Percentage = $83\%$
Answer: The percentage of marks obtained by Ambika in the aggregate of all the subjects is $83\%$.
Question 127. What sum of money lent out at 16 per cent per annum simple interest would produce ₹ 9600 as interest in 2 years?
Answer:
Given:
Rate of Interest (R) = $16\%$ per annum
Simple Interest (SI) = $\textsf{₹} \ 9600$
Time (T) = $2$ years
To Find:
The sum of money lent out (Principal, P).
Solution:
The formula for calculating Simple Interest is:
$SI = \frac{P \times R \times T}{100}$
Where P is the Principal amount, R is the Rate of interest, and T is the Time period in years.
We need to find the Principal (P). We can rearrange the formula to solve for P:
$P = \frac{SI \times 100}{R \times T}$
Substitute the given values into the formula:
$P = \frac{9600 \times 100}{16 \times 2}$
$P = \frac{960000}{32}$
Now, perform the division:
$P = 30000$
The sum of money lent out is $\textsf{₹} \ 30,000$.
Answer: The sum of money lent out was $\textsf{₹} \ 30,000$.
Question 128. Harish bought a gas-chullah for ₹ 900 and later sold it to Archana at a profit of 5 per cent. Archana used it for a period of two years and later sold it to Babita at a loss of 20 per cent. For how much did Babita get it?
Answer:
Given:
Cost Price for Harish (CP for Harish) = $\textsf{₹} \ 900$
Profit percentage for Harish = $5\%$
Archana sold it at a loss of $20\%$.
To Find:
The price at which Babita bought the gas-chullah.
Solution:
First, calculate the price at which Harish sold the gas-chullah to Archana. This is the Selling Price for Harish (SP for Harish).
SP for Harish = CP for Harish + Profit
Profit = $5\%$ of CP for Harish
Profit = $\frac{5}{100} \times 900 = 0.05 \times 900 = \textsf{₹} \ 45$
SP for Harish = $900 + 45 = \textsf{₹} \ 945$
So, Archana bought the gas-chullah for $\textsf{₹} \ 945$. This is the Cost Price for Archana (CP for Archana).
CP for Archana = $\textsf{₹} \ 945$
Archana sold the gas-chullah to Babita at a loss of $20\%$. The time Archana used it (2 years) is not relevant for the price calculation.
Loss percentage for Archana = $20\%$
Loss amount for Archana = $20\%$ of CP for Archana
Loss amount = $\frac{20}{100} \times 945 = 0.20 \times 945 = \textsf{₹} \ 189$
The price at which Archana sold the gas-chullah to Babita is the Selling Price for Archana (SP for Archana).
SP for Archana = CP for Archana - Loss amount
SP for Archana = $945 - 189 = \textsf{₹} \ 756$
The price at which Archana sold it is the price at which Babita got it.
Price for Babita = SP for Archana = $\textsf{₹} \ 756$
Answer: Babita got the gas-chullah for $\textsf{₹} \ 756$.
Question 129. Match each of the entries in Column I with the appropriate entries in Column II:
Column I
(i) 3:5
(ii) 2.5
(iii) 100%
(iv) $\frac{2}{3}$
(v) $6\frac{1}{4}$ %
(vi) 12.5 %
(vii) SP when CP = ₹ 50 and loss = 6 %
(viii) SP when CP = ₹ 50 and profit = ₹ 4
(ix) Profit% when CP = ₹ 40 and SP = ₹ 50
(x) Profit% when CP = ₹ 50 and SP = ₹ 60
(xi) Interest when principal = ₹ 800, Rate of interest = 10% per annum and period = 2 years
(xii) Amount when principal = ₹ 150, Rate of interest = 6% per annum and period = 1 year
Column II
(A) ₹ 54
(B) ₹ 47
(C) ₹ 53
(D) ₹ 160
(E) 60 %
(F) 25 %
(G) $\frac{1}{16}$
(H) 250 %
(I) ₹ 159
(J) $66\frac{2}{3}$ %
(K) 20 %
(L) 0. 125
(M) 3 : 2
(N) ₹ 164
(O) 3 : 3
Answer:
Given:
Entries in Column I and Column II as listed in the question.
To Find:
Match each entry in Column I with the appropriate entry in Column II.
Solution:
We calculate the value of each entry in Column I and find its corresponding value in Column II.
(i) $3:5 = \frac{3}{5} = 0.6$. As a percentage, $0.6 \times 100\% = 60\%$. This matches Column II (E).
(ii) $2.5$. As a percentage, $2.5 \times 100\% = 250\%$. This matches Column II (H).
(iii) $100\%$. This is equal to $1$. In the context of ratios, this can be represented as $1:1$. The ratio $3:3$ in Column II (O) simplifies to $1:1$. Thus, this matches Column II (O).
(iv) $\frac{2}{3}$. As a percentage, $\frac{2}{3} \times 100\% = \frac{200}{3}\% = 66\frac{2}{3}\%$. This matches Column II (J).
(v) $6\frac{1}{4}\% = \frac{25}{4}\%$. As a fraction, $\frac{25/4}{100} = \frac{25}{400} = \frac{1}{16}$. This matches Column II (G).
(vi) $12.5\% = \frac{12.5}{100} = \frac{125}{1000} = 0.125$. This matches Column II (L).
(vii) SP when CP = $\textsf{₹} \ 50$ and loss = $6\%$. Loss amount $= 6\%$ of $\textsf{₹} \ 50 = \frac{6}{100} \times 50 = \textsf{₹} \ 3$. SP $= CP - \text{Loss} = 50 - 3 = \textsf{₹} \ 47$. This matches Column II (B).
(viii) SP when CP = $\textsf{₹} \ 50$ and profit = $\textsf{₹} \ 4$. SP $= CP + \text{Profit} = 50 + 4 = \textsf{₹} \ 54$. This matches Column II (A).
(ix) Profit% when CP = $\textsf{₹} \ 40$ and SP = $\textsf{₹} \ 50$. Profit $= SP - CP = 50 - 40 = \textsf{₹} \ 10$. Profit% $= \left(\frac{\text{Profit}}{CP}\right) \times 100\% = \left(\frac{10}{40}\right) \times 100\% = \frac{1}{4} \times 100\% = 25\%$. This matches Column II (F).
(x) Profit% when CP = $\textsf{₹} \ 50$ and SP = $\textsf{₹} \ 60$. Profit $= SP - CP = 60 - 50 = \textsf{₹} \ 10$. Profit% $= \left(\frac{\text{Profit}}{CP}\right) \times 100\% = \left(\frac{10}{50}\right) \times 100\% = \frac{1}{5} \times 100\% = 20\%$. This matches Column II (K).
(xi) Interest when principal = $\textsf{₹} \ 800$, Rate = $10\%$ p.a., Period = $2$ years. SI $= \frac{P \times R \times T}{100} = \frac{800 \times 10 \times 2}{100} = 8 \times 10 \times 2 = \textsf{₹} \ 160$. This matches Column II (D).
(xii) Amount when principal = $\textsf{₹} \ 150$, Rate = $6\%$ p.a., Period = $1$ year. Interest $= \frac{150 \times 6 \times 1}{100} = \frac{900}{100} = \textsf{₹} \ 9$. Amount $= \text{Principal} + \text{Interest} = 150 + 9 = \textsf{₹} \ 159$. This matches Column II (I).
Answer:
(i) - (E)
(ii) - (H)
(iii) - (O)
(iv) - (J)
(v) - (G)
(vi) - (L)
(vii) - (B)
(viii) - (A)
(ix) - (F)
(x) - (K)
(xi) - (D)
(xii) - (I)
Question 130. In a debate competition, the judges decide that 20 per cent of the total marks would be given for accent and presentation. 60 per cent of the rest are reserved for the subject matter and the rest are for rebuttal. If this means 8 marks for rebuttal, then find the total marks.
Answer:
Given:
Percentage for accent and presentation = $20\%$ of total marks.
Percentage for subject matter = $60\%$ of the remaining marks (after deducting accent and presentation marks).
Marks for rebuttal = $8$ marks.
The remaining marks (after deducting accent/presentation and subject matter marks) are for rebuttal.
To Find:
The total marks.
Solution:
Let the total marks be $T$.
Percentage of marks for accent and presentation = $20\%$ of $T$.
Marks remaining after allotting for accent and presentation = $100\% - 20\% = 80\%$ of the total marks.
Marks for subject matter = $60\%$ of the remaining $80\%$.
Percentage for subject matter = $60\%$ of $80\%$
Percentage for subject matter = $\frac{60}{100} \times 80\% = 0.60 \times 80\% = 48\%$ of the total marks.
The marks for rebuttal are the rest of the marks.
Percentage for rebuttal = Total Percentage - Percentage for accent/presentation - Percentage for subject matter
Percentage for rebuttal = $100\% - 20\% - 48\% = 32\%$ of the total marks.
We are given that the marks for rebuttal are $8$.
So, $32\%$ of the total marks ($T$) is equal to $8$ marks.
$32\% \text{ of } T = 8$
Write the percentage as a decimal or fraction:
$\frac{32}{100} \times T = 8$
$0.32 \times T = 8$
To find $T$, divide $8$ by $0.32$:
$T = \frac{8}{0.32}$
$T = \frac{8}{\frac{32}{100}} = \frac{8 \times 100}{32}$
$T = \frac{800}{32}$
Simplify the fraction:
$T = \frac{\cancel{800}^{25}}{\cancel{32}_{1}} \text{ (Dividing both by 32)}$
$T = 25$
The total marks are $25$.
Answer: The total marks are $25$.
Question 131. Divide ₹ 10000 in two parts so that the simple interest on the first part for 4 years at 12 per cent per annum may be equal to the simple interest on the second part for 4.5 years at 16 per cent per annum.
Answer:
Given:
Total amount to be divided = $\textsf{₹} \ 10000$
For the first part:
Time ($T_1$) = $4$ years
Rate of Interest ($R_1$) = $12\%$ per annum
For the second part:
Time ($T_2$) = $4.5$ years
Rate of Interest ($R_2$) = $16\%$ per annum
Condition: Simple Interest on the first part = Simple Interest on the second part.
To Find:
The two parts of $\textsf{₹} \ 10000$.
Solution:
Let the first part be $\textsf{₹} \ P_1$ and the second part be $\textsf{₹} \ P_2$.
The total amount is the sum of the two parts:
$P_1 + P_2 = 10000$
We can express $P_2$ in terms of $P_1$: $P_2 = 10000 - P_1$.
The formula for Simple Interest is $SI = \frac{P \times R \times T}{100}$.
Simple Interest on the first part ($SI_1$) is:
$SI_1 = \frac{P_1 \times R_1 \times T_1}{100} = \frac{P_1 \times 12 \times 4}{100} = \frac{48 P_1}{100} = 0.48 P_1$
Simple Interest on the second part ($SI_2$) is:
$SI_2 = \frac{P_2 \times R_2 \times T_2}{100} = \frac{P_2 \times 16 \times 4.5}{100} = \frac{16 \times 4.5 P_2}{100}$
$16 \times 4.5 = 16 \times \frac{9}{2} = 8 \times 9 = 72$
$SI_2 = \frac{72 P_2}{100} = 0.72 P_2$
According to the condition given in the problem, $SI_1 = SI_2$:
$0.48 P_1 = 0.72 P_2$
Substitute $P_2 = 10000 - P_1$ into the equation:
$0.48 P_1 = 0.72 (10000 - P_1)$
$0.48 P_1 = 0.72 \times 10000 - 0.72 P_1$
$0.48 P_1 = 7200 - 0.72 P_1$
Add $0.72 P_1$ to both sides of the equation:
$0.48 P_1 + 0.72 P_1 = 7200$
$(0.48 + 0.72) P_1 = 7200$
$1.20 P_1 = 7200$
Solve for $P_1$:
$P_1 = \frac{7200}{1.20}$
$P_1 = \frac{7200}{\frac{120}{100}} = \frac{7200 \times 100}{120}$
$P_1 = \frac{720000}{120} = \frac{72000}{12}$
$P_1 = 6000$
So, the first part is $\textsf{₹} \ 6000$.
Now find the second part using $P_2 = 10000 - P_1$:
$P_2 = 10000 - 6000$
$P_2 = 4000$
The second part is $\textsf{₹} \ 4000$.
Verification:
$SI_1 = \frac{6000 \times 12 \times 4}{100} = 60 \times 12 \times 4 = 60 \times 48 = 2880$
$SI_2 = \frac{4000 \times 16 \times 4.5}{100} = 40 \times 16 \times 4.5 = 40 \times 72 = 2880$
Since $SI_1 = SI_2 = \textsf{₹} \ 2880$, the division is correct.
Answer: The sum of $\textsf{₹} \ 10000$ is divided into two parts: $\textsf{₹} \ 6000$ and $\textsf{₹} \ 4000$.
Question 132. ₹ 9000 becomes ₹ 18000 at simple interest in 8 years. Find the rate per cent per annum.
Answer:
Given:
Principal amount (P) = $\textsf{₹} \ 9000$
Amount after 8 years (A) = $\textsf{₹} \ 18000$
Time period (T) = $8$ years
Type of interest = Simple Interest
To Find:
The rate of interest (R) per cent per annum.
Solution:
The Amount (A) is the sum of the Principal (P) and the Simple Interest (SI).
$A = P + SI$
We can find the Simple Interest by subtracting the Principal from the Amount:
$SI = A - P$
$SI = \textsf{₹} \ 18000 - \textsf{₹} \ 9000$
$SI = \textsf{₹} \ 9000$
The formula for Simple Interest is:
$SI = \frac{P \times R \times T}{100}$
We need to find the Rate of Interest (R). Rearranging the formula to solve for R:
$R = \frac{SI \times 100}{P \times T}$
Substitute the calculated Simple Interest and the given values of Principal and Time into the formula:
$R = \frac{9000 \times 100}{9000 \times 8}$
$R = \frac{900000}{72000}$
Cancel out the common zeros from the numerator and the denominator:
$R = \frac{900}{72}$
Simplify the fraction by dividing both numerator and denominator by their common factors. We can divide by 9:
$R = \frac{900 \div 9}{72 \div 9} = \frac{100}{8}$
Further simplify by dividing by 4:
$R = \frac{100 \div 4}{8 \div 4} = \frac{25}{2}$
Convert the fraction to a decimal:
$R = 12.5$
The rate per cent per annum is $12.5\%$.
Answer: The rate per cent per annum is $12.5\%$.
Question 133. In how many years will the simple interest on a certain sum be 4.05 times the principal at 13.5 per cent per annum?
Answer:
Given:
Simple Interest ($SI$) is $4.05$ times the Principal ($P$). So, $SI = 4.05 \times P$.
Rate of Interest ($R$) = $13.5\%$ per annum.
To Find:
The time period ($T$) in years.
Solution:
The formula for Simple Interest is:
$SI = \frac{P \times R \times T}{100}$
Substitute the given information into the formula. We know $SI = 4.05 P$ and $R = 13.5$:
$4.05 \times P = \frac{P \times 13.5 \times T}{100}$
Since the Principal ($P$) is on both sides of the equation (and $P$ cannot be zero for interest to be earned), we can divide both sides by $P$:
$4.05 = \frac{13.5 \times T}{100}$
Now, we need to solve for $T$. Multiply both sides of the equation by $100$:
$4.05 \times 100 = 13.5 \times T$
$405 = 13.5 \times T$
Divide both sides by $13.5$ to find $T$:
$T = \frac{405}{13.5}$
To perform the division with a decimal, multiply the numerator and the denominator by $10$ to remove the decimal point from the denominator:
$T = \frac{405 \times 10}{13.5 \times 10} = \frac{4050}{135}$
Now, divide $4050$ by $135$:
$T = 30$
The time period is $30$ years.
Answer: The simple interest on a certain sum will be $4.05$ times the principal in $30$ years.
Question 134. The simple interest on a certain sum for 8 years at 12 per cent per annum is ₹ 3120 more than the simple interest on the same sum for 5 years at 14 per cent per annum. Find the sum.
Answer:
Given:
Let the certain sum (Principal) be $\textsf{₹} \ P$.
Scenario 1:
Time ($T_1$) = $8$ years
Rate of Interest ($R_1$) = $12\%$ per annum
Scenario 2:
Time ($T_2$) = $5$ years
Rate of Interest ($R_2$) = $14\%$ per annum
Condition: Simple Interest in Scenario 1 ($SI_1$) is $\textsf{₹} \ 3120$ more than Simple Interest in Scenario 2 ($SI_2$).
To Find:
The sum (Principal, P).
Solution:
The formula for Simple Interest (SI) is $SI = \frac{P \times R \times T}{100}$.
Calculate the Simple Interest in Scenario 1 ($SI_1$):
$SI_1 = \frac{P \times R_1 \times T_1}{100} = \frac{P \times 12 \times 8}{100} = \frac{96 P}{100} = 0.96 P$
Calculate the Simple Interest in Scenario 2 ($SI_2$):
$SI_2 = \frac{P \times R_2 \times T_2}{100} = \frac{P \times 14 \times 5}{100} = \frac{70 P}{100} = 0.70 P$
According to the given condition:
$SI_1 = SI_2 + 3120$
Substitute the expressions for $SI_1$ and $SI_2$ into the equation:
$0.96 P = 0.70 P + 3120$
Subtract $0.70 P$ from both sides of the equation:
$0.96 P - 0.70 P = 3120$
Combine the terms with $P$:
$(0.96 - 0.70) P = 3120$
$0.26 P = 3120$
Solve for $P$ by dividing both sides by $0.26$:
$P = \frac{3120}{0.26}$
To perform the division, multiply the numerator and denominator by 100 to remove the decimal:
$P = \frac{3120 \times 100}{0.26 \times 100} = \frac{312000}{26}$
Perform the division:
$P = 12000$
The certain sum (Principal) is $\textsf{₹} \ 12000$.
Answer: The sum is $\textsf{₹} \ 12000$.
Question 135. The simple interest on a certain sum for 2.5 years at 12 per cent per annum is ₹ 300 less than the simple interest on the same sum for 4.5 years at 8 per cent per annum. Find the sum.
Answer:
Given:
Let the certain sum (Principal) be $\textsf{₹} \ P$.
Scenario 1:
Time ($T_1$) = $2.5$ years
Rate of Interest ($R_1$) = $12\%$ per annum
Scenario 2:
Time ($T_2$) = $4.5$ years
Rate of Interest ($R_2$) = $8\%$ per annum
Condition: Simple Interest in Scenario 1 ($SI_1$) is $\textsf{₹} \ 300$ less than Simple Interest in Scenario 2 ($SI_2$). This means $SI_2 - SI_1 = 300$.
To Find:
The sum (Principal, P).
Solution:
The formula for Simple Interest (SI) is $SI = \frac{P \times R \times T}{100}$.
Calculate the Simple Interest in Scenario 1 ($SI_1$):
$SI_1 = \frac{P \times R_1 \times T_1}{100}$
$SI_1 = \frac{P \times 12 \times 2.5}{100}$
$SI_1 = \frac{P \times 30}{100} = 0.30 P$
Calculate the Simple Interest in Scenario 2 ($SI_2$):
$SI_2 = \frac{P \times R_2 \times T_2}{100}$
$SI_2 = \frac{P \times 8 \times 4.5}{100}$
$SI_2 = \frac{P \times 36}{100} = 0.36 P$
According to the given condition, the difference between the two simple interests is $\textsf{₹} \ 300$, and $SI_2$ is greater than $SI_1$:
$SI_2 - SI_1 = 300$
Substitute the expressions for $SI_1$ and $SI_2$ into the equation:
$0.36 P - 0.30 P = 300$
Combine the terms with $P$:
$(0.36 - 0.30) P = 300$
$0.06 P = 300$
Solve for $P$ by dividing both sides by $0.06$:
$P = \frac{300}{0.06}$
To perform the division, multiply the numerator and denominator by 100 to remove the decimal from the denominator:
$P = \frac{300 \times 100}{0.06 \times 100} = \frac{30000}{6}$
Perform the division:
$P = 5000$
The certain sum (Principal) is $\textsf{₹} \ 5000$.
Verification:
$SI_1 = 0.30 \times 5000 = 1500$
$SI_2 = 0.36 \times 5000 = 1800$
$SI_2 - SI_1 = 1800 - 1500 = 300$. This matches the given condition.
Answer: The sum is $\textsf{₹} \ 5000$.
Question 136. Designing a Healthy Diet
When you design your healthy diet, you want to make sure that you meet the dietary requirements to help you grow into a healthy adult.
As you plan your menu, follow the following guidelines
1. Calculate your ideal weight as per your height from the table given at the end of this question.
2. An active child should eat around 55.11 calories for each kilogram desired weight.
3. 55 per cent of calories should come from carbohydrates. There are 4 calories in each gram of carbohydrates.
4. 15 per cent of your calories should come from proteins. There are 4 calories in each gram of proteins.
5. 30 per cent of your calories may come from fats. There are 9 calories in each gram of fat.
Following is an example to design your own healthy diet.
Example
1. Ideal weight = 40 kg.
2. The number of calories needed = 40 × 55.11 = 2204.4
3. Calories that should come from carbohydrates = 2204.4 × 0.55 = 1212.42 calories.
Therefore, required quantity of carbohydrates = $\frac{1212.42}{4}$ = 303.105g = 300 g. (approx).
4. Calories that should come from proteins = 2204.4 × 0.15 = 330.66 calories.
Therefore, required quantity of protein = $\frac{330.66}{4}$ g = 82.66 g.
5. Calories that may come from fat = 2204.4 × 0.3 = 661.3 calories.
Therefore, required quantity of fat = $\frac{661.3}{9}$ g = 73.47 g.
Answer the Given Questions
1. Your ideal desired weight is __________ kg.
2. The quantity of calories you need to eat is _______.
3. The quantity of protein needed is ________ g.
4. The quantity of fat required is ___________ g.
5. The quantity of carbohydrates required is __________ g.
Answer:
Given:
Guidelines for designing a healthy diet and a table showing ideal weight for height.
To Find:
The required quantities based on your ideal weight, according to the given questions.
Solution:
To answer the questions, you first need to determine your ideal desired weight from the provided table based on your height and gender. Since your specific height and gender are not provided in the input, I will demonstrate the process using an assumed ideal weight. Let's assume an ideal desired weight of $45$ kg for the purpose of calculation.
Step 1: Find Ideal Weight
Refer to the table in the image titled "Ideal Weight for Height for Boys and Girls". Locate your height (in feet and inches) and find the corresponding ideal weight (in kg) for your gender. Write this value down for Question 1.
For demonstration, let's assume Ideal Desired Weight = $45$ kg.
Step 2: Calculate Total Calories Needed
Use Guideline 2:
Total Calories Needed = Ideal Weight (kg) $\times$ $55.11$ (calories/kg)
Total Calories Needed = $45 \times 55.11$
$45 \times 55.11 = 2479.95$ calories.
This is the answer for Question 2.
Step 3: Calculate Quantity of Protein Needed
Use Guideline 4 to find calories from proteins, then convert to grams:
Calories from Proteins = Total Calories Needed $\times$ $15\%$
Calories from Proteins = $2479.95 \times \frac{15}{100} = 2479.95 \times 0.15$
$2479.95 \times 0.15 \approx 371.99$ calories.
Convert calories to grams using the fact that there are 4 calories in each gram of protein:
Quantity of Protein Needed = $\frac{\text{Calories from Proteins}}{4 \text{ calories/gram}}$
Quantity of Protein Needed = $\frac{371.99}{4} \approx 92.998$ grams.
Approximately $93$ g (rounding to one decimal place or nearest whole number may be appropriate depending on context, but let's keep a couple of decimals).
This is the answer for Question 3.
Step 4: Calculate Quantity of Fat Required
Use Guideline 5 to find calories from fats, then convert to grams:
Calories from Fats = Total Calories Needed $\times$ $30\%$
Calories from Fats = $2479.95 \times \frac{30}{100} = 2479.95 \times 0.30$
$2479.95 \times 0.30 \approx 743.985$ calories.
Convert calories to grams using the fact that there are 9 calories in each gram of fat:
Quantity of Fat Required = $\frac{\text{Calories from Fats}}{9 \text{ calories/gram}}$
Quantity of Fat Required = $\frac{743.985}{9} \approx 82.665$ grams.
Approximately $82.67$ g (rounding to one decimal place or nearest whole number may be appropriate depending on context, but let's keep a couple of decimals).
This is the answer for Question 4.
Step 5: Calculate Quantity of Carbohydrates Required
Use Guideline 3 to find calories from carbohydrates, then convert to grams:
Calories from Carbohydrates = Total Calories Needed $\times$ $55\%$
Calories from Carbohydrates = $2479.95 \times \frac{55}{100} = 2479.95 \times 0.55$
$2479.95 \times 0.55 \approx 1363.9725$ calories.
Convert calories to grams using the fact that there are 4 calories in each gram of carbohydrates:
Quantity of Carbohydrates Required = $\frac{\text{Calories from Carbohydrates}}{4 \text{ calories/gram}}$
Quantity of Carbohydrates Required = $\frac{1363.9725}{4} \approx 340.993$ grams.
Approximately $341.0$ g (rounding to one decimal place or nearest whole number may be appropriate depending on context, but let's keep a couple of decimals).
This is the answer for Question 5.
Answer:
Please find your ideal weight from the table using your height and gender. Then follow the steps above with your ideal weight.
Using an assumed ideal desired weight of $45$ kg as an example:
1. Your ideal desired weight is $\underline{45}$ kg.
2. The quantity of calories you need to eat is $\underline{2479.95}$.
3. The quantity of protein needed is $\underline{\approx 93.0}$ g.
4. The quantity of fat required is $\underline{\approx 82.67}$ g.
5. The quantity of carbohydrates required is $\underline{\approx 341.0}$ g.
(Note: These answers are based on an assumed ideal weight of 45 kg. Your answers will vary based on your actual ideal weight from the table.)
Question 137. 150 students are studying English, Maths or both. 62 per cent of students study English and 68 per cent are studying Maths. How many students are studying both?
Answer:
Given:
Total number of students studying English, Maths, or both = $150$
Percentage of students studying English = $62\%$
Percentage of students studying Maths = $68\%$
To Find:
The number of students studying both English and Maths.
Solution:
Let the total number of students be $N = 150$.
The percentage of students studying English is $P(E) = 62\%$.
The percentage of students studying Maths is $P(M) = 68\%$.
Since all $150$ students are studying at least one of the subjects (English or Maths or both), the percentage of students studying English or Maths or both is $100\%$.
We can use the principle of inclusion-exclusion for percentages:
Percentage studying (English or Maths or Both) = Percentage studying English + Percentage studying Maths - Percentage studying Both
$P(E \cup M) = P(E) + P(M) - P(E \cap M)$
We know $P(E \cup M) = 100\%$, $P(E) = 62\%$, and $P(M) = 68\%$.
$100\% = 62\% + 68\% - P(E \cap M)$
$100\% = 130\% - P(E \cap M)$
Rearranging the equation to find the percentage studying both ($P(E \cap M)$):
$P(E \cap M) = 130\% - 100\%$
$P(E \cap M) = 30\%$
So, $30\%$ of the total students study both English and Maths.
Now, calculate the number of students studying both:
Number of students studying both = $30\%$ of Total students
Number of students studying both = $\frac{30}{100} \times 150$
Number of students studying both = $0.30 \times 150$
Number of students studying both = $45$
Answer: $45$ students are studying both English and Maths.
Question 138. Earth Science: The table lists the world’s 10 largest deserts.
| Largest Desert in the World | |
|---|---|
| Desert | Area (km 2) |
| Sahara (Africa) | 8,800,000 |
| Gobi (Asia) | 1,300,000 |
| Australian Desert (Australia) | 1,250,000 |
| Arabian Desert (Asia) | 850,000 |
| Kalahari Desert (Africa) | 580,000 |
| Chihuahuan Desert (North America) | 370,000 |
| Takla Makan Desert (Asia) | 320,000 |
| Kara Kum (Asia) | 310,000 |
| Namib Desert (Africa) | 310,000 |
| Thar Desert (Asia) | 260,000 |
(a) What are the mean, median and mode of the areas listed?
(b) How many times the size of the Gobi Desert is the Namib Desert?
(c) What percentage of the deserts listed are in Asia?
(d) What percentage of the total area of the deserts listed is in Asia?
Answer:
Given:
A table listing the areas of the 10 largest deserts in the world.
To Find:
(a) The mean, median, and mode of the listed areas.
(b) The ratio of the size of the Namib Desert to the size of the Gobi Desert.
(c) The percentage of the listed deserts that are in Asia.
(d) The percentage of the total area of the listed deserts that is in Asia.
Solution:
The areas listed are (in km$\$^2$): 8,800,000, 1,300,000, 1,250,000, 850,000, 580,000, 370,000, 320,000, 310,000, 310,000, 260,000.
Total number of deserts listed is $10$.
Part (a): Mean, Median, and Mode
To find the Mean, sum all the areas and divide by the number of deserts:
Sum of Areas = $8800000 + 1300000 + 1250000 + 850000 + 580000 + 370000 + 320000 + 310000 + 310000 + 260000 = 14350000$ km$\$^2$.
Mean = $\frac{\text{Sum of Areas}}{\text{Number of Deserts}} = \frac{14350000}{10} = 1435000$ km$\$^2$.
To find the Median, arrange the areas in ascending order and find the middle value. Since there are 10 values (an even number), the median is the average of the 5th and 6th values.
Areas in ascending order: 260,000, 310,000, 310,000, 320,000, 370,000, 580,000, 850,000, 1,250,000, 1,300,000, 8,800,000.
5th value = 370,000 km$\$^2$.
6th value = 580,000 km$\$^2$.
Median = $\frac{370000 + 580000}{2} = \frac{950000}{2} = 475000$ km$\$^2$.
To find the Mode, identify the area that appears most frequently in the list.
The area 310,000 km$\$^2$ appears twice, while all other areas appear only once.
Mode = 310,000 km$\$^2$.
Part (b): Namib Desert vs Gobi Desert
Area of Gobi Desert = 1,300,000 km$\$^2$.
Area of Namib Desert = 310,000 km$\$^2$.
The question asks "How many times the size of the Gobi Desert is the Namib Desert?", which means calculating the ratio $\frac{\text{Area of Namib}}{\text{Area of Gobi}}$.
Ratio = $\frac{310000}{1300000} = \frac{31}{130}$.
The Namib Desert is $\frac{31}{130}$ times the size of the Gobi Desert.
Part (c): Percentage of Deserts in Asia
Count the number of deserts located in Asia from the table:
Gobi (Asia), Arabian Desert (Asia), Takla Makan Desert (Asia), Kara Kum (Asia), Thar Desert (Asia).
Number of deserts in Asia = $5$.
Total number of deserts listed = $10$.
Percentage of deserts in Asia = $\left(\frac{\text{Number of Asian Deserts}}{\text{Total Number of Deserts}}\right) \times 100\%$
Percentage = $\left(\frac{5}{10}\right) \times 100\% = \frac{1}{2} \times 100\% = 50\%$.
Part (d): Percentage of Total Area in Asia
Calculate the total area of deserts located in Asia:
Area of Asian Deserts = $1300000 + 850000 + 320000 + 310000 + 260000 = 3040000$ km$\$^2$.
Total area of all listed deserts = $14350000$ km$\$^2$ (calculated in part a).
Percentage of total area in Asia = $\left(\frac{\text{Total Area of Asian Deserts}}{\text{Total Area of All Deserts}}\right) \times 100\%$
Percentage = $\left(\frac{3040000}{14350000}\right) \times 100\% = \left(\frac{304}{1435}\right) \times 100\%$.
$\frac{304}{1435} \times 100 = \frac{30400}{1435}$.
Performing the division: $\frac{30400}{1435} \approx 21.1846...$
Percentage $\approx 21.18\%$.
Answer:
(a) The mean area is $1,435,000$ km$\$^2$. The median area is $475,000$ km$\$^2$. The mode area is $310,000$ km$\$^2$.
(b) The Namib Desert is $\frac{31}{130}$ times the size of the Gobi Desert.
(c) $50\%$ of the deserts listed are in Asia.
(d) Approximately $21.18\%$ of the total area of the deserts listed is in Asia.
Question 139. Geography Application: Earth’s total land area is about 148428950 km2. The land area of Asia is about 30 per cent of this total. What is the approximate land area of Asia to the nearest square km?
Answer:
Given:
Earth's total land area = $148428950$ km$\$^2$.
Land area of Asia = $30\%$ of Earth's total land area.
To Find:
The approximate land area of Asia to the nearest square km.
Solution:
We need to calculate $30\%$ of the Earth's total land area.
Land area of Asia = $30\%$ of $148428950$ km$\$^2$.
Land area of Asia = $\frac{30}{100} \times 148428950$
Land area of Asia = $0.30 \times 148428950$
Performing the multiplication:
$0.30 \times 148428950 = 44528685$
The land area of Asia is approximately $44528685$ km$\$^2$.
The question asks for the approximate land area to the nearest square km. Since the calculated area is already an integer, rounding to the nearest square km gives the same value.
Answer: The approximate land area of Asia to the nearest square km is $44528685$ km$\$^2$.
Question 140. The pieces of Tangrams have been rearranged to make the given shape.

By observing the given shape, answer the following questions:
- What percentage of total has been coloured?
(i) Red (R) = _________
(ii) Blue (B) = ________
(iii) Green (G) = _______
- Check that the sum of all the percentages calculated above should be 100.
- If we rearrange the same pieces to form some other shape, will the percentatge of colours change?
Answer:
Given:
A shape made by rearranging Tangram pieces, with different pieces coloured Red, Blue, and Green.
To Find:
(i) The percentage of the total area coloured Red.
(ii) The percentage of the total area coloured Blue.
(iii) The percentage of the total area coloured Green.
Check if the sum of these percentages is $100\%$.
Determine if the percentages change when the pieces are rearranged into a different shape.
Solution:
A standard Tangram set consists of 7 pieces that form a square. The areas of these pieces relative to the total area of the square are fixed:
2 large right triangles: each is $\frac{1}{4}$ of the total area.
1 medium right triangle: $\frac{1}{8}$ of the total area.
2 small right triangles: each is $\frac{1}{16}$ of the total area.
1 square: $\frac{1}{8}$ of the total area.
1 parallelogram: $\frac{1}{8}$ of the total area.
Total Area = $2 \times \frac{1}{4} + 1 \times \frac{1}{8} + 2 \times \frac{1}{16} + 1 \times \frac{1}{8} + 1 \times \frac{1}{8} = \frac{1}{2} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} = \frac{4+1+1+1+1}{8} = \frac{8}{8} = 1$ (representing $100\%$ of the area).
From the given image, we can identify which pieces correspond to each color:
Red (R) consists of: 1 large triangle, 1 square, and 1 small triangle.
Blue (B) consists of: 1 medium triangle and 1 parallelogram.
Green (G) consists of: 1 large triangle and 1 small triangle.
Now, let's calculate the total area for each color as a fraction of the total area:
Area of Red = (Area of large triangle) + (Area of square) + (Area of small triangle)
Area of Red = $\frac{1}{4} + \frac{1}{8} + \frac{1}{16} = \frac{4}{16} + \frac{2}{16} + \frac{1}{16} = \frac{7}{16}$ of the total area.
Area of Blue = (Area of medium triangle) + (Area of parallelogram)
Area of Blue = $\frac{1}{8} + \frac{1}{8} = \frac{2}{8} = \frac{1}{4}$ of the total area.
Area of Green = (Area of large triangle) + (Area of small triangle)
Area of Green = $\frac{1}{4} + \frac{1}{16} = \frac{4}{16} + \frac{1}{16} = \frac{5}{16}$ of the total area.
Now, convert these fractions to percentages:
Percentage of Red = $\left(\frac{7}{16}\right) \times 100\% = \frac{700}{16}\% = \frac{175}{4}\% = 43.75\%$
Percentage of Blue = $\left(\frac{1}{4}\right) \times 100\% = 25\%$
Percentage of Green = $\left(\frac{5}{16}\right) \times 100\% = \frac{500}{16}\% = \frac{125}{4}\% = 31.25\%$
The percentages of total area coloured are:
(i) Red (R) = $43.75\%$
(ii) Blue (B) = $25\%$
(iii) Green (G) = $31.25\%$
Check the sum of the percentages:
Sum = $43.75\% + 25\% + 31.25\% = 68.75\% + 31.25\% = 100\%$
The sum of all the percentages is $100\%$.
If we rearrange the same pieces to form some other shape, will the percentage of colours change?
No, the percentage of colours will not change. The total area covered by each colour is determined by the specific Tangram pieces that are painted that colour. When these exact same pieces are rearranged, their individual areas do not change, and thus the sum of the areas for each colour remains constant. The total area of the figure formed by all 7 pieces also remains constant. Therefore, the percentage of each colour relative to the total area stays the same, regardless of the shape formed.
Answer:
(i) Red (R) = $43.75\%$
(ii) Blue (B) = $25\%$
(iii) Green (G) = $31.25\%$
Check: $43.75\% + 25\% + 31.25\% = 100\%$. The sum is $100\%$.
If we rearrange the same pieces to form some other shape, the percentage of colours will not change.

